製造業なんかでは、工程能力指数とかXbar-R管理図を使う事で、工程の状態を把握する事が出来、管理状態の置くことが出来ます。
ですが、これらを始めとした統計的手法には、大抵一つの前提条件が必要になる事が多いです。
それは、正規分布である事
これです。
通常は、ヒストグラムを描いて、その形状から判断する事が推奨されます。
しかしながら、分布の区切り位置の取り方なんかで、色々な形になってしまうのもあるし、判断の尺度が与えられていないので、実は運用が難しいです。
以下の図が正規分布に従っているかと聞かれたら、どう答えますか?
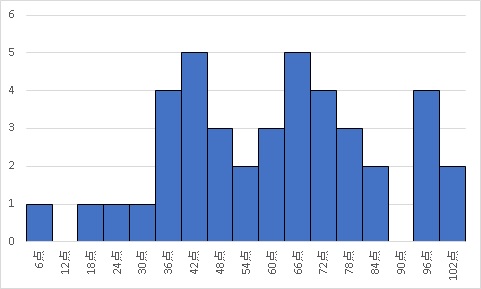
なんか自身持てないですよね?
だから、もっと明確に判断する方法、例えば検定とかないのか?
という要望は、当然持たれるでしょう。
という事で、今回は正規分布か否か、つまり正規性を判定する代表的な検定、シャピロ-ウィルク検定の概要とEZRでの実用方法を紹介いたします。
今回はこちらの本を参考にしていますが、正直ガチの大学生向けで、難易度が高すぎるんであまりお勧めはしません。
それでも、興味があるって方だけ読んでみて下さい。
正規性の検定 シャピロ-ウィルク検定

正規性の分析は、実は相当難しい分野
そもそも、そんな検定の方法があるのであれば、絶対必要だし、便利だし統計的工程管理の教科書でも出てきてもいいじゃないか。
私は初めそう思ってました。
多分、これを読んでくださっているアナタも同じ気持ちだと思うんです。
ですが、これが教科書においそれと載らない理由があります。
それは、かなり難しいからです。
順序統計量とか概念が出てくるので、数学を専門的にやってきていない人間には、理論を理解するのはとても無理です。
だから、初級向けの教科書とかには、とても載せられないのです。
ですが、安心してください。
難しいのは理論であって、実用は非常に簡単です。
今回は、シャピロ-ウィルク検定の概念だけに触れて、実用についてはEZRで実施していきます。
データを入れて、ポチポチっとすればほぼ秒で結果が出てくるので、ラクチンですよ。
まずはQ-Qプロットを描こう
シャピロ-ウィルク検定を実施する前には、必ずQ-Qプロットで確認する事をお勧めします。
というのも、そもそもシャピローウィルク検定では、Q-Qプロットが直線に従っているのかを見ているからです。
なので、概要を理解するには、まずQ-Qプロットのおさらいから始めましょう。
Q-Qプロットとは、実測値を対象に
・実際に発生した確率
・正規分布に従って発生した場合の確率
を比較して、比例の関係になるかどうかを描画するグラフです。
実際に発生した確率が正規分布で仮定する確率なら、正規分布であると言えるわけです。
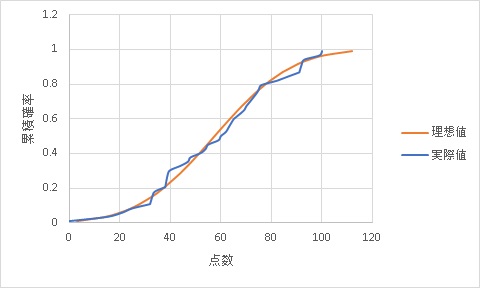
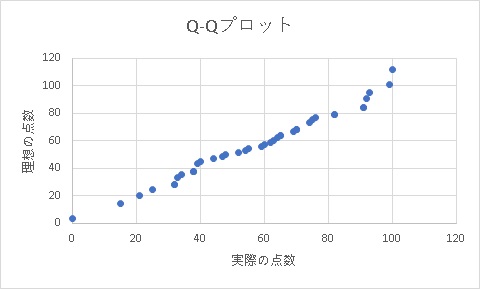
理想(正規分布)と現実(実測値)の比例状態を見るので、Q-Qプロットが直線に近ければ正規分布であると言えます。
Q-Qプロットの詳細が知りたい方は、コチラの記事を参照ください。
さて、Q-Qプロットが直線に近ければ、正規分布であると言える。
なら、Q-Qプロットが直線であることを判定してくれる検定があれば、最強じゃね?
という発想は当然浮かぶわけです。
そこで、シャピロ-ウィルク検定の出番なわけです。
シャピロ-ウィルク検定の概要
シャピロ-ウィルク検定は、とても難しいお話なので、概要だけさらっと触れます。
基本的には、決定係数の変形になります。
決定係数とは、単回帰式がどれだけ精度が高いかを示す指標です。
$$r^2=\frac{[\frac{1}{N}\sum(x-\overline{x})(y-\overline{y})]^2}{\frac{1}{N}\sum(x-\overline{x})^2\frac{1}{N}\sum(y-\overline{y})^2}$$
ここのxとyに、実際の点数と理想の点数(正規分布に従う)をぶち込む感じです。
ちなみに、ここから色々変形させていくと、シャピロ-ウィルク検定の統計量
$$W=\frac{(\sum_{i=1}^n{b_{ni}X_{(i)}})}{\sum_{i=1}^n(X_i-\overline{X})^2}$$
ただし、
$$b_n=[b_{n1}・・・b_{nn}]^T=\frac{1}{\sqrt{a_n^TV^{-1}V^{-1}a_n}}a_n^TV^{-1}$$
$$V=[v_{ij}],v_ij=E[(Z_{(i)}-a_{ni})(Z_{(j)}-a_{nj})$$
どう考えても、このブログで扱うレベルを超えちゃってますね。
とりあえず、本質はQ-Qプロットに対して決定係数を算出して、その値に対して検定を行っていると理解しておけば大丈夫です。
シャピロ-ウィルク検定をやってみよう

まずはQ-Qプロットまで出してみる
シャピロ-ウィルク検定は、Q-Qプロットの直線性を見る検定ですので、まずはQ-Qプロットを出します。
今回は以下のデータとヒストグラムに対して、実施してみました。

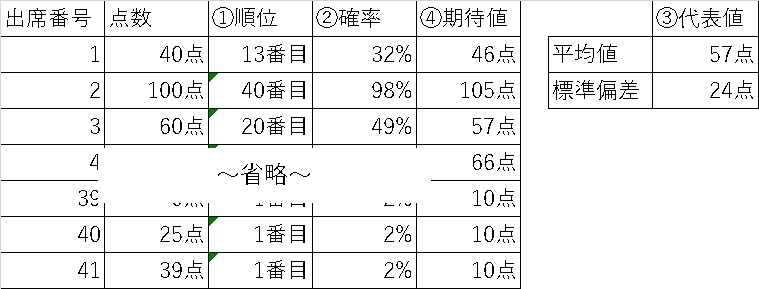
これだけだと、正規分布と言えるのか微妙なところです。
これらのデータをEZRにぶち込んで、Q-Qプロットを選択します。
すると、Q-Qプロットが描画されます。
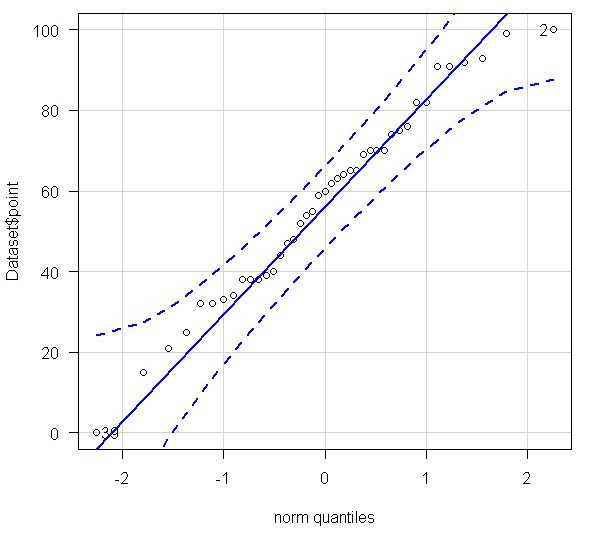
詳細はQ-Qプロットの過去記事参照(同じデータについて扱っています)
このQ-Qプロットをみるに、かなり正規分布と言い切れるほどに直線に見えます。
ですが、まだ目視確認ですので、ここから検定を行う事で、有意差の有無を確認します。
ちなみに、正規性の検定の帰無仮説H0、対立仮説H1は
$$H0:正規分布と一致している$$
$$H1:正規分布と一致していない$$
になりますので、(正規分布と)有意差なしの判定で、正規分布であると言えます。
つまり、P値が0.05(もしくは0.01)より、大きかったら正規分布です。
まず、データをインポートしたら、
次に[Shapiro-Wilk]を選択して、OKします。
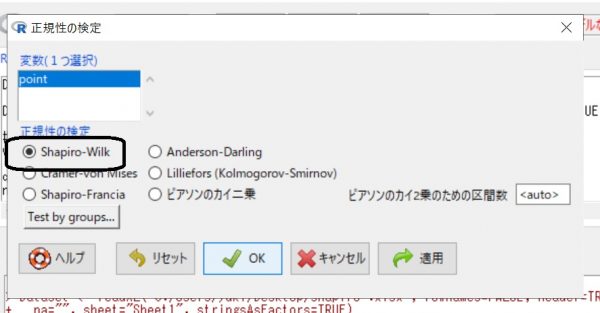
すると、【出力】の方にこのような表示が出ます。
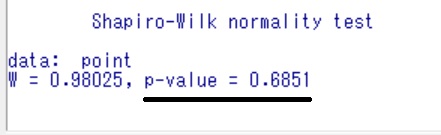
注目すべきは、P値(p-value)です。
正規分布であることは、P値があらかじめ決めた有意水準(大抵α=0.05)以上である必要があります。
今回はP値が0.6851と0.05と比較して、大きいので有意差なし。
つまり、正規分布であるという事が言えます。
以上です。
いかがですか?理論は難しいですが、運用は簡単でしょ?
EZR(やR commander)は無料な上、Rの知識も全く必要ないので、インストールしたらすぐにこの分析は実行できます。
エクセルでは無理な分析が簡単に出来るようになるので、ぜひインストールしてみてださい。
正規性の検定の注意事項
正規性を判断する上で、検定という手段は非常に便利です。
やはりグラフの形で判断するよりも、有意差ありなしで判定してくれた方が楽ですからね。
ですが、シャピロ-ウィルクを始めとした正規性の検定には、一つ欠点があります。
それは、有意差なし=正規分布である点です。
そもそも、検定というものは、有意差なしを積極的には採択出来ないという特性があります。
故に、検定の結果で有意差なしと出ても、本当に正規分布であるかは、結構怪しいのです。
それではどうすれば良いのでしょうか?
一番手っ取り早いのは、やはりQ-Qプロットとの併用です。
Q-Qプロットで、ほぼ直線を描いている上で、検定の結果でも正規分布であると出たならば、まず間違いなく正規分布と判断して良いでしょう。
このように、統計の手法はそれぞれ弱点が存在しますので、単一の手法に依存するのではなく、複数の手法を併用する事が望ましいです。
特にグラフとそれに関連する検定の組み合わせは、非常に強力なのでおススメです。
まとめ
統計的手法を使う際には、しばしば正規分布であるかどうかが、分析のカギになります。
ヒストグラムだけだと、どうしても難しいところがあるので、そんなときにはQ-Qプロットとシャピロ-ウィルク検定を実施するのが良いです。
検定の理論はとても難しいですが、ざっくり言えばQ-Qプロットが直線に従っているかを検定しています。
また、実用に関してはEZRを使えば非常に簡単に導き出せます。
Q-Qプロット⇒シャピロ-ウィルク検定の流れは、カップラーメンよりも早く分析出来ますので、スピードに追われるビジネスにおいても非常に実用的です。
ぜひ、一度使ってみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント
Great content! Super high-quality! Keep it up! 🙂