製造業に携わっていると、『工程能力指数(以下Cpk)』という数値に出くわすことがあります。
自信が勤める会社で算出しているのなら良いのですが、お客さんから
「Cpkを1.33以上維持できていますか?」
といきなり言われた場合は困りものです。
えっ何それ?と社内がざわつくはずです。
しかもそれまでCpkを意識していなかった場合、まず満足のいくCpkで作れていることはないでしょうし、いきなり言われてCpkを上げるということも極めて難しいはずです。
なぜならば、Cpkは平均値と標準偏差から構成される指標であり、平均値はともかく標準偏差(つまり”ばらつき”)を是正することは容易ではないからです。
普段社内でCpkを意識していない、聞いたことがないということは、QC手法に接したことがない可能性が高く、標準偏差を考慮した管理が出来ていない可能性が高いということになります。
そういった場合、管理値は平均値や最大/最小値からなんとなく作ったものである可能性が高く管理状態にない可能性が高いということになるわけです。
これは逆に考えると、皆さんの仕入先の材料品質が疑わしい場合
「この材料のこの項目のCpkを教えてください」
と尋ねて狼狽えたり、提出に時間が掛かったりした場合は、管理状態にない可能性が濃厚になると言えます。
試しにカマかけしてみては如何でしょうか。
話が若干逸れましたが、今回はそんなCpkの解説をしていきたいと思います。
動画解説もアップしています。こちらもぜひご参考ください。
Cpkとは何を表しているのか?
Cpkは工程の管理状態を表した指標になります。この数値が高いほど工程は管理された状態であると言えます。
ではなぜ数値が高いと管理されていると言えるのか。それは式の構造を見ていくと分かります。
まずはCpを算出しましょう
Cpkを算出するにはまず、Cpを算出する必要があります。Cpとは以下の式で算出される値です。
$$Cp=\frac{(UCL-LCL)}{6σ}$$
UCL(Upper Class Line)は上限規格、LCL(Lower Class Line)は下限規格を指します。
σは標準偏差です。
この式は上下限規格と品質の分布の関係を図示すると、非常に理解しやすくなります。
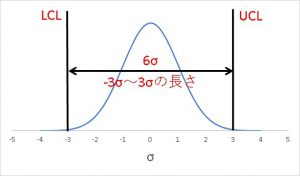
6σとはつまり-3σ~3σを表しているのです。±3σがぴったりUCL~LCLの規格内に収まっているとその比(つまりCp)は1になります。
そして、6σの値が小さくなる(“ばらつき”が小さくなるほど)Cpの値は大きくなります。
Cpの最適値は1.33
Cp(及びCpk)の最適値は1.33です。
これは実は±4σに相当します。
この1.33に6σを掛けてみましょう。
$$1.33×6σ=7.98σ≒8σ$$
8σとは-4σ~4σに相当します。これは規格外れが出る確率が0.006%であることを意味します。
1.33以上のCpk(5σや6σ相当)は、過剰品質であり品質が多少下がっても良いのでコストを下げるべきであると言われる領域になります。

つまりCp(及びCpk)を維持出来ているかと問われることは
「不良率0.006%の工程を維持出来ているか?」
と問われることに等しいということです。
CpからCpkへ
しかしながら、ここまでのCpには問題点があります。
それは平均値、つまり分布の中央の位置づけを考慮していないという点です。
平均値が規格の中心に位置していれば、Cpは正しいと言えますが実際は規格の中心からずれている事が多いです。
そこで、平均値の中心からのずれを補正する必要があります。
偏りを司る『K』
この偏りを補正する値Kの式は、以下になります。
$$K=\frac{|(UCL+LCL)/2-μ|}{(UCL-LCL)/2}$$
UCLは上限規格、LCLは下限規格、μは平均値です。
この式ですが、
分子(UCL+LCL)/2は規格の中央を表しています。つまり分子の部分は中央に対しての平均値のズレを表しています。
そして絶対値に変換しますので、大きくなるほど規格中心からのズレが大きいことを示しています。
分母(UCL-LCL)/2は規格の大きさの半分を表しています。
規格の半分でズレを割ることで、汎用的に使用出来る比率に変換しています。
そしてこのKをCpに組み込む式は以下になります。
$$Cpk=(1-K)Cp$$
これで、平均値の規格からのズレも考慮した工程能力指数Cpkが算出されます。
片側規格の場合
先程のCpkは両側規格の場合です。
上限規格及び下限規格の場合は、算出方法が少し異なります。
上限規格の場合
$$Cpk=\frac{(UCL-μ)}{3σ}$$
下限規格の場合
$$Cpk=\frac{(μ-LCL)}{3σ}$$
構造的に、両側規格の時のCpを平均値をもとに半分にぶった切ったような形になっています。
これらの式は、平均値μを式に組み入れているために偏りが考慮されています。つまりそれぞれにKの計算は必要ありません。
また、両側規格の場合でも上限規格の場合、下限規格の場合のCpkを算出して小さい方を採用するという方法もあります。
まとめ
Cpkの算出方法を紹介しました。
このように式の構造を知っていると、どういう意味の数値か分かってきます。
またこのように式の構造を抑えておくと、品質が悪い場合に
・”ばらつき”を抑えるべきなのか
・平均値のズレを修正するべきなのか
実行すべきアクションが適切に選択できます。
現場の数字をこのように統計的に判断できるようになったら、かなりのスキルアップに繋がります。
せっかく役立つ数値ですから、お客さんに文句を言われるだけの迷惑なものと思わず、積極的に活用していきましょう。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント