検定は有意差を知るための、代表的な統計学の手法です。
基本的に仕事で気になるのは、平均値の有意差ですがおそらくそれと同じくらいに気になるのが、“ばらつき”の有意差だと思います。
という事で今回はばらつきの検定である、F検定を紹介していきます。
このF検定は様々な場面で活用する機会がありますから、ぜひ使えるようになってください。
動画でも解説しています。
参考になったら、ぜひチャンネル登録とグッド評価をお願いします。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
F検定って何？
F値とは？
まず気になる事があると思います。
F検定のFって何？
って事です。
これはこの手法を作った(というか推計統計学のパパ)R.A.フィッシャーのFです。
そしてこのF検定では
・F値
とそのF値がとる
・F分布
を使用して検定を行います。
という事で、まずはF値を解説いたします。
F値というのは、ズバリ分散の比です。式は以下の通り
$$F=\frac{σ_1^2}{σ_2^2}$$
そしてこのF値を算出するときには、一つ決め事があります。それは
・分散の小さい方を分母に持ってくる
という事です。これは分散同士に差が生じると、分母に対して分子が大きくなっていくので
・1を最小にどんどん大きくなる
という事を意味しています。
F値が大きくなると、ばらつきに差が有るという事です。
そしてF値が一定の値(有意水準)以上になったら、有意差があるとするのがF検定なのです。
F分布とは
そしてF値がとる標本分布がF分布です。
こんな感じの分布になります。
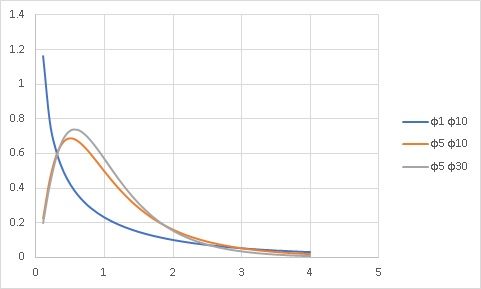
F分布は2つの分散、それぞれの自由度で形状が決定します。
故に当然、一定のF値でも自由度(=サンプルサイズ)によって検定の結果は変わってくるのです。
このような自由度で分布の形状が変化して、精度に追従するところなんかはt分布にそっくりです。
なので、教科書ではF分布表を見ながら条件に合う自由度の、各有意水準を探していくことになりますが、
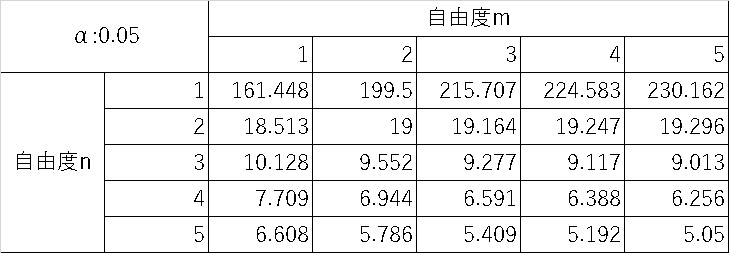
正直とっても面倒くさいので、実務ではエクセルの分析ツールや関数(F.TEST関数)でp値を導き出す方が早いです。
ですが、それらのツールを使うにしても、F検定の方法を知っておかなければとんでもないミスを犯す可能性も出てきますので、ぜひF検定の方法を学習していってください。
F検定の方法とは？
検定の進め方について
基本的な検定の進め方ですが、F検定に限らず全て
・帰無仮説/対立仮説を立てる
・有意水準を決める
・検定統計量(今回はF値)を算出
・有意水準に相当する分布の値を検索
・分布の値と検定統計量を比較し、帰無仮説を棄却可能か確認
となっています。以下の記事及びyoutubeでも解説していますので、参照ください。
F検定の進め方
それではやっていきましょう。
①まず帰無仮説と対立仮説を立てます。
帰無仮説 H0:σA2=σB2
対立仮説 H1:σA2≠σB2
です。
②有意水準を決めます。5%とすることが一般的です。厳しめにしたい場合は1%を使用する事もあります。
③次にF値を算出します。
$$F_0=\frac{σ_A^2}{σ_B^2}$$
この時に使う分散値は不偏分散を使用します。
③F分布表を確認します。
F分布は、有意水準ごとに準備されており、分布Aと分布Bそれぞれの自由度(サンプルサイズn-1)の交点の値を確認します。
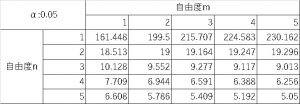
例えば、分布Aの自由度が3で、分布Bの自由度が5の場合は、F=5.409になります。
④F値の比較をします。
不偏分散の比として算出したF0とF分布表から取ってきたFを比較して、
$$F_0 > F$$
の場合、帰無仮説：分散が等しい場合に生じる可能性5%以下となり、帰無仮説は正しくないとされ、「対立仮説：分散は等しくない」が採択されます。
逆に
$$F_0 < F$$
の場合は、帰無仮説は棄却されず、「帰無仮説：分散は等しい」可能性があるという結果となります。(帰無仮説は棄却出来なかったとしても、採択することはできません)
エクセル関数で実施する場合
以上までが基本的なF検定の流れですが、F分布表を片手に一々やっていられないという所が本音だと思います。
なので実際にはエクセルの関数F.TESTを使いましょう。
=F.TEST(配列1,配列2)
配列1,2には、分散(=ばらつき)を比較したいサンプルデータを選択します。
すると、p値が算出されますので、有意水準と比較して有意差の有無を確認出来ます。
例えば有意水準を0.05としていた場合、F.TESTが返す結果が0.05を下回れば有意差ありで2つのデータのばらつきには有意差がある事が示せます。
このように非常に簡単ですので、ぜひ使用してみて下さい。
まとめ
F検定は分散の差を判断するための手法です。
F値という分散比を、F分布を利用して検定を行います。
F検定も通常の検定の例に漏れず、帰無仮説～有意性の判断までは他の検定と同様です。
F検定はばらつきの有意差を判断するために使用され、またその性質を利用して分散分析にも使われます。
分散分析を使いこなす上でも、F検定は必須スキルになりますので、ぜひマスターしていきましょう。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ！」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます！！
買い切りタイプなのでお得です。
ぜひお求めくださいな。
コメント