統計的手法はその多くが、対象とする分布が正規分布していることを前提としています。
そのため、標本が正規分布しているかどうかは、極めて重要です。
正規性の検証で有名どころはシャピロ-ウィルク検定や尖度、歪度の検定などがありますが、最も代表的なものはQ-Qプロットでしょう。
Q-Qプロットは数ある正規性の検証手法の中で、おそらく最も理解しやすいものと思っています。
エクセルでの検証は面倒ですが、EZRだと簡単に出来ます。
それでは行きましょう!
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
Q-Qプロットとは?
正規分布を累積分布関数で捉える
Q-Qプロットで中心となるのは、累積分布関数になった正規分布です。
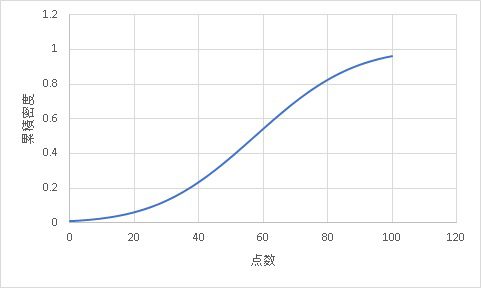
累積分布関数とは、小さい確率変数から大きい確率変数へ確率を積み上げていく(累積)していく関数で、0%に近いところから始まり、最終的に100%付近で飽和します。
Q-Qプロットは、実際の数字で描いた累積分布と平均値/標準偏差から描かれる理想の累積分布を照らし合わせたグラフになります。
Q-Qプロットを作ってみよう
実際にQ-Qプロットを作ってみます。

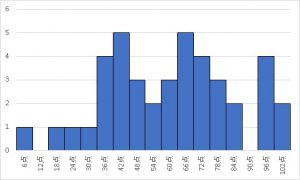
この41人のテストの点数が正規分布しているか見てみましょう。
ヒストグラムは以下の記事で紹介した方法で作成しています。
手順として、まずはこの実際の点数を累積分布関数にすることから始まります。
基本的に、各数字に順位をつけてその順位から累積確率を導き出します。
①各点数を小さい順に並び替えた時の、順番を付ける。
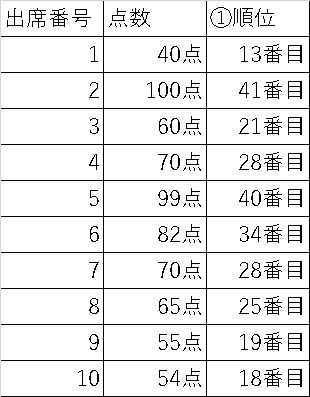
②以下の式でその順位に該当する累積確率値を割りだします。
$$確率=\frac{順位-1/2}{N}$$
これで順位と累積確率が準備出来ました。
必要はないのですが試しに、この数字で累積分布を描画してみましょう。以下のようになります。
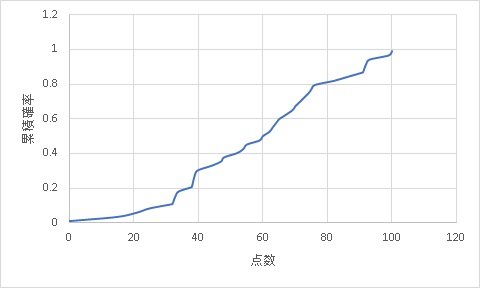
次に平均値、標準偏差から割り出される理想的な正規分布の累積分布を導き出しましょう。
④平均値、標準偏差から正規分布を作った場合の累積密度関数において、各確率値ごとの期待値を算出します(エクセルならNORM.INV関数で算出可能です)。
これらを算出した一覧が以下になります。
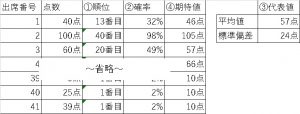
理想の正規分布の累積分布を追記すると以下になります。
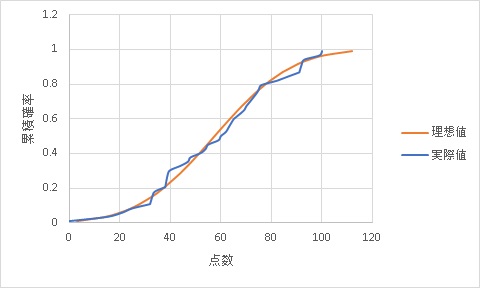
理想と実際の値にそれほどギャップが無さそうに見えます。
さて、大詰めです。
最後に実際の点数と理想の点数の散布図を作成します。
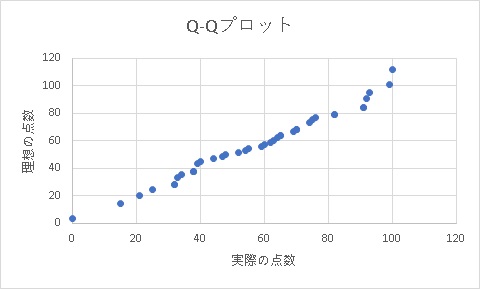
これでQ-Qプロットの完成です。
Q-Qプロットの見方
Q-Qプロットは実測値と理想値(正規分布)をプロットしたものです。
よって直線であれば、実測値は理想値に近く正規分布であると言えるのです。
今回作ったQ-Qプロットはかなり直線に近いと言えるので、正規分布としても良さそうです。
Q-Qプロットの問題点
Q-Qプロットは直線であるかどうかを確認するという、単純な見方で判別できる方法ですが、どの程度なら正規分布であるとはっきり言うことが出来ない点が欠点であると言えます。
基本的には他の正規性分析と照らし合わせたりするのが良いでしょう。
EZRを使ったQ-Qプロット
エクセルではかなり煩雑な作業が多かったですが、EZRを使えばかなり簡単に作図することが可能です。
Q-Qプロットの作図方法
まずEZRを開き、データをインポートします。
そして、グラフと表を選びその中のQQプロットを選びます。
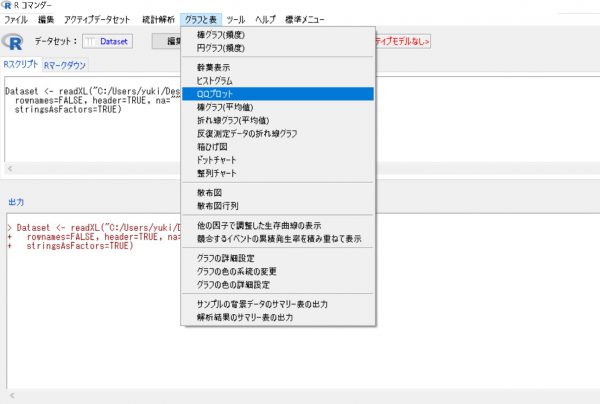
あとは、正規性分析する変数(今回はpoint=点数)を選択し、正規にチェックがついた状態でOKをクリックしてください。
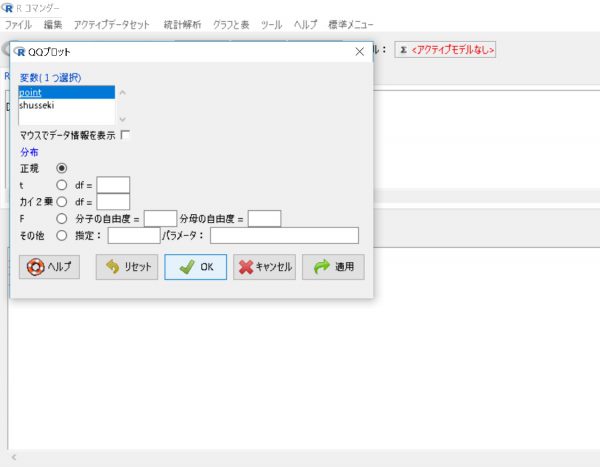
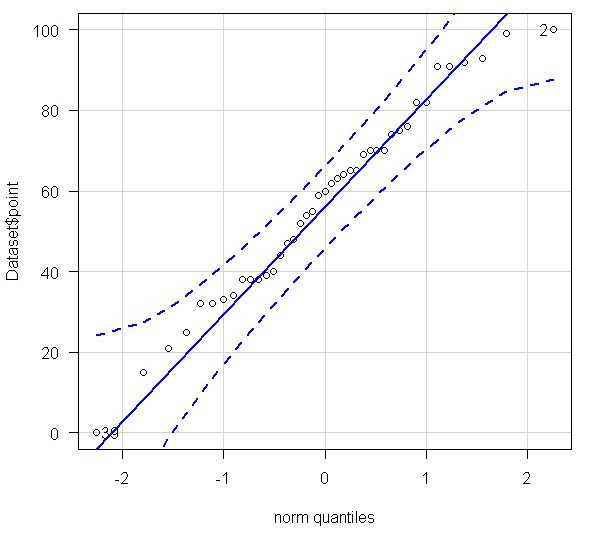
これで以下のグラフが作図されます。
 おしまいです。
おしまいです。
EZRでのQ-Qプロット
EZRでQ-Qプロットを実施すると、直線の目安とどこに収まるべきかの破線が自動で描画されるので、正規性があるかどうかの判別がかなり容易です。
手順も簡単ですので、実際の運用時はEZRで行うのが良いでしょう(ただ内容を理解する為に一度はエクセルでやってみることをお勧めします)。
まとめ
このQ-Qプロットは、確率変数と期待値を確率で橋渡しした場合にどれだけ一致するかを見ることで、正規性を確認するグラフです。
今回の事例はヒストグラムを作図した状態では、正規分布か分からない状態でした。
ヒストグラムは級間隔と級数の取り方で、その印象がガラリと変わるものなので、ヒストグラムだけで判断というのは避けましょう。
EZRを使えば、確認も5分以下で終わりますし直線の補助線もあって判断しやすいです。
Q-Qプロットによる正規性の確認をマスター出来れば、工程能力指数や管理図を遺憾なく利用出来るようになります。この辺りの正規分布を前提とした手法のネックがやはり
「これ正規分布なのか?」
ってところなので、ここを押さえる事が出来ればあなたの統計リテラシーはかなり向上し、市場価値もかなり高まると言えるでしょう。
またEZRにはほかの正規性検定もデフォルトで搭載されているので、併せて実施すれば判断を間違えることはないでしょう(シャピロ・ウィルク検定がQ-Qプロットの検定版なので相性が良い)。
正規性の判断は、統計学で重要でありながらも、その実非常に難易度が高いものが多いです。
これをマスターして、正しい統計を実践していきましょう。
今回使った元データのエクセルファイルはコチラです。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント