製造現場で管理データを測定したり、研究開発のためにデータを測定するとき、皆さんは
「この測定器、大丈夫かな？」
と気にすることはありますでしょうか？
少なくともISOなどを取得している場合、製造現場の測定器は定期的に点検・校正はしているかもしれません。
しかしながら、点検・校正は飽くまで測定器を確認するだけで、測定システムは評価出来ていません。
また、更に言えば技術者は、そもそも測定機器の精度を疑う機会すらあまりないかもしれません。
データの”ばらつき”が大きくても相応にサンプルサイズを大きくして、平均値だけを押さえるだけでOKと考えているかもしれないからです。
しかし、これでは良くありません。
正しくない測定システムでは、そもそも当サイトで紹介しているような統計的手法を扱う事すら覚束ないはずです。
さながら、筆で米粒に文字を書くが如しです。米より大きな筆先では、如何な達人であろうとも文字を書くことは叶いません。
そこで、今回は測定システムの評価する手法、ゲージR&R(以下GR&R)について解説していきます。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
GR&Rとは
測定システムの評価方法
GR&Rの話はいる前に、まず測定システムについて解説します。
測定システムは、測定器だけではなく、それを扱う方法、人のスキルなど測定に関わる全てを含みます。
つまり、測定器がいくら定期校正され、狂いがなくとも、測定方法がおかしかったり、測定者のスキルが不十分である場合、正しく測定されないという事です。
今回紹介するGR&Rは、測定器だけでなく、測定する人(というより測定器以外の要因)全てを評価することが出来ます。
繰返し性と再現性
GR&Rは
Gage Repetability and Reproducibility = 測定器 繰返し性と再現性
の略です。ここで言う繰返し性と再現性とは
・繰返し性：測定器要因の変動
・再現性：測定者要因(もしくは測定器以外)の変動
の事を言います。データのばらつきとは、
$$データの変動=EV+AV+PV$$
で成立します。ここで
EV：繰返し性(測定器変動)
AV：再現性(測定者変動)
PV：部品変動
GR&R：EV+AV
となります。
このGR&Rには、以下のような合否判定基準があります。
GR&R < 10%：合格
10% ≦ GR&R < 30%：ある適用について合格(コストバランス、顧客の承認要)
30% ≦ GR&R：不合格
このように明確に合否が数字として表れるので、曖昧な解釈が入り込む余地がなく非常に扱いやすいのです。
二元配置分散分析でGR&R
この複数の要因の変動を評価するという手法は、分散分析そのものです。
GR&Rでは、平均-範囲法とANOVA(分散分析)法の2種類があるのですが、精度の問題や分散分析の延長で考えることが出来ることを考慮し、当サイトではANOVA法で考えていきます。
基本的な流れとしては、
・10pcsのサンプルを3人の測定者が3回ずつ測定する
・繰り返しのある二元配置分散分析法を実施する
・交互作用は有意差なしの場合、その変動、自由度は誤差に合計する。有意差ありの場合は交互作用の値は無視する
・二元配置分散分析の値をGR&Rの各式に当てはめ変換する
・GR&Rを評価する。
という流れになります。二元配置分散分析に関しては以下の記事を参照ください。
GR&Rの公式
GR&Rへの変換公式は以下になります。
交互作用がある場合
$$EV=\sqrt{誤差分散}$$
$$AV=\sqrt{\frac{測定者分散-誤差分散}{部品数×繰返し数}}$$
$$PV=\sqrt{\frac{部品分散-誤差分散}{繰返し数×測定者数}}$$
$$GRR=\sqrt{EV^2+AV^2}$$
$$TV=\sqrt{GRR^2+PV^2}$$
交互作用がない場合は、
$$V_{pool}=\frac{誤差変動+交互作用変動}{誤差自由度+交互作用自由度}$$
$$EV=\sqrt{V_{pool}}$$
$$AV=\sqrt{\frac{測定者分散-V_{pool}}{部品数×繰返し数}}$$
$$PV=\sqrt{\frac{部品分散-V_{pool}}{繰返し数×測定者数}}$$
$$GRR=\sqrt{EV^2+AV^2}$$
$$TV=\sqrt{GRR^2+PV^2}$$
そしてGR&R/TVのパーセンテージで合否を判定します。
GR&Rを計算してみよう
実際に計算してみましょう。
測定システムを評価する為に、以下のようなデータを採取しました。
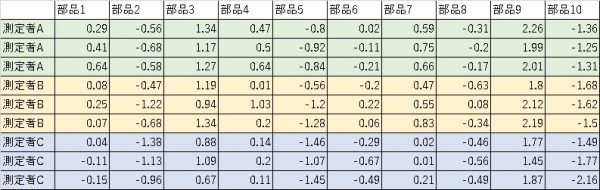
こちらをエクセルの分析ツールで二元配置分散分析を実施した結果、以下のような結果となりました。
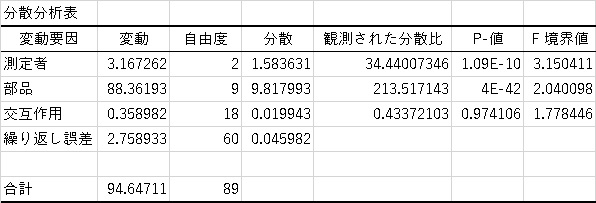
この表から交互作用には、有意差が認められないので繰り返し誤差と交互作用の変動と自由度を合算します。表を整えると
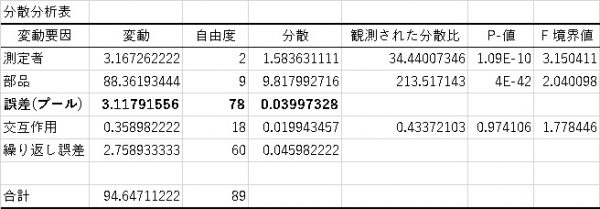
ここからGR&Rのそれぞれの値を算出します。
$$EV=\sqrt{0.04}=0.20$$
$$AV=\sqrt{\frac{1.58-0.04}{3×10}}=0.23$$
$$PV=\sqrt{\frac{9.818-0.04}{3×3}}=1.04$$
$$GRR=\sqrt{0.20^2+0.23^2}=0.30$$
$$TV=\sqrt{0.30^2+1.04^2}=1.09$$
となります。そしてすべての値をTVで割ると、合否判定の数字が割り出せます。
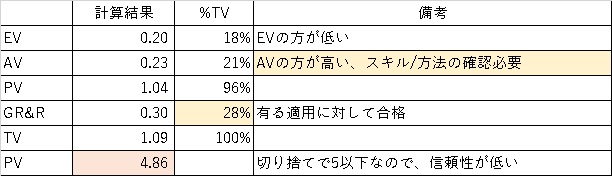
一覧にするとこうなります。
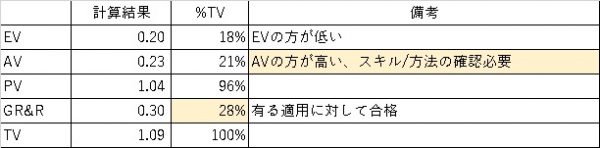
この結果からGR&Rの値は、30%以下であり、使えないことはないといった結果になります。
そして、ここからが肝心なのですが、EVとAVの値を比較することで、どちらに非があるのかを判断することが出来ます。
例えばEVの%が高い場合は、点検・校正がなされていない可能性があります。
対してAVの%が高い場合には、測定方法か測定者のスキル不足などソフト面での不具合が生じている可能性があります。
このようにGR&Rを行えば、測定システムの合否だけでなく改善の糸口も見つけ出すことが出来ます。
補足：知覚区分数
GR&Rを実施する場合には、サンプルにはある程度の”ばらつき”が必要とされています。
その”ばらつき”の規模は通常の管理値を超えるものも、評価対象として加えるレベルです。
基本的には、不良品や品種違いを測定対象に含めることを推奨しています。
サンプルばらつきが小さすぎると、測定システムの評価が過小になってしまう為です。
そしてこれを評価する指標が知覚区分数です。以下の式で表されます。
$$ndc=1.41\frac{PV}{GRR}$$
このndcが切り捨てで5未満の場合、信頼性に欠けるとされています。
今回の例の場合
であり、切り捨てで4になるのでイマイチこの結果の信頼性は薄いと言えます。
まとめ
GR&Rで測定システムを評価することで、今の数字が正しいかどうか、そして悪い場合はどこを直すべきかを知ることが出来ます。
そして、”ばらつき”が少ない測定システムを使用することで必然的に必要なサンプルサイズを減らすことが出来、コスト削減にも直結します。
GR&RやMSAを使いこなせる人は結構稀です。
極めて効果の高いツールですので、ぜひ活用してみてください。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ！」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます！！
買い切りタイプなのでお得です。
ぜひお求めくださいな。
コメント