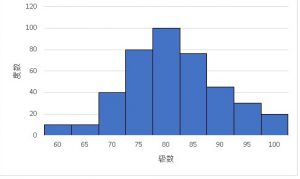
ヒストグラムは以下のような、横軸に級数、縦軸に度数をとったグラフのことです。
例えば選挙の投票数について、各年代100人ずつにアンケートを取ったとします。そのデータを使って年齢別の投票率の分布を図示したい場合は、以下のようになります(数字そのものはでたらめです。悪しからず)。
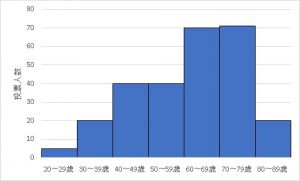
この場合、横軸にある10歳単位(20~29歳)で級数を取り、その年代の投票数を合計しています。
このヒストグラムは、平均値と標準偏差のみで表現される正規分布よりも、実態に近い分布の形を示してくれる便利なグラフです。
一見すると、作図も簡単そうに見えます。
しかしながら、実は意外と作成が難しいグラフです。
何が難しいのか?それは級の間隔です。
例えば、投票数のグラフの級の間隔は10ですが、これを30にしてみます。
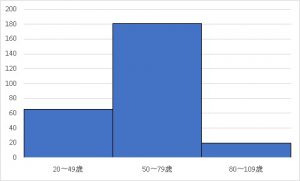
直感的にも、正しい分布を捉えていないと分かって頂けるはずです。
このように、級の間隔の取り方を変えるだけで、グラフの印象はガラリと変わります。
年代別グラフなど区切りをイメージしやすいデータなら良いですが、例えば200世帯のある一か月の電気使用量というような、どこで区切りをつけるべきかイメージがつきにくいデータの場合は、非常に難しくなります。
そんなヒストグラムですが、正しく作図するためのアウトラインというものがあります。
①級の間隔を適切に決める
②級間隔を均一にする
③級の境界を明確にする
④級内で度数の集中点がある場合、その点が級中央にくるようにする。
一つずつ見ていきましょう。
youtubeにもアップしています。
①級の間隔を適切に決める
特に決まったルールはないのですが、一つの指針としてスタージスという人が作った以下の公式があります。
適当な級数をm、データ数をnとした場合
$$m≒1+\frac{\log_{10} n}{\log_{10} 2}≒1+3.32\log_{10} n$$
そしてデータの最大値-最小値(これを範囲といいます)をRとした場合、級間隔cは
$$c≒\frac{R}{m}$$
で近似されます。
これに当てはめれば適当な級数、級間隔を迷わず決定出来ます。
②級間隔を均一にする
これは当然といえば当然なのですが、級間隔を広くすればその分度数は大きくなり、逆に狭くすれば度数は小さくなるので真の分布の形が分からなくなります。
級の間隔は①で決めた内容で統一しましょう。
③級の境界を明確にする
例えば級を0~50、50~100などと示した場合、50の度数はどちらに入れたらいいか、もしくはどちらに入っているのか分からなくなります。
ですので、0以上50未満、50以上100未満など明確に分かる形で表記する必要があります。
④級内で度数の集中点がある場合、その点が級中央にくるようにする。
これは一見何を言っているかわかりづらいと思います。例えばあるデータがあって、そのデータは5の倍数(5,10,15…)で度数が大きくなるようなデータであったりするとします。
そのような場合、級の取り方を
0~5、6~10、11~15…
とするのではなく、
3~7、8~12、13~17
のように5の倍数が各級の真ん中にくるように区切りを決めよということです。
これは各級の真ん中の数値が最頻値であろうという考えに基づきます。
つまり3~7の範囲で正規分布が描かれており、その場合中央が最頻値になるはずということです。
これは逆にヒストグラムから平均値を導き出す場合にも用いる前提になりますので、覚えておくと便利です。
以上ヒストグラムを作る場合には4つアウトラインがあり、これに従うと正しいヒストグラムを作ることが出来ます。
また提供されたヒストグラム(分析結果、成績書等)を確認する場合にも、この原則に従って作図されているかを確認することで、正しくデータが提示されているかを洞察することが出来ます。
以上のアウトラインをれるせいき押さえて、作図スキルと分析スキルを高めていきましょう。



コメント