そのデータがどのような分布をしているのかを知るためには、ヒストグラムを作るのが一番です。
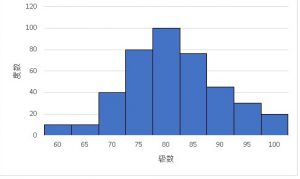
という事で、私なんかはよく材料メーカーから度数分布表やヒストグラム表を貰ったりすることがあるんですが、不親切なところだと
平均値や標準偏差が記載されていない
なんていう衝撃的な状態で提出されることがあります。
度数分布表やヒストグラムに記載されている情報というモノは、集計値であり、生データではありません。
また、折角ヒストグラムが正規分布を形成していても、統計量が分からなければ、どの程度の確率で、どのような外れ値が発生するのか、全く分からないのです。
このような場合、そりゃ相手に統計量を教えろと言ったり、今後は記載するように叱り飛ばすのも手ですが、それでもあまり真面目に応じてくれないという可能性もなくはないです。
そういう時の為に、度数分布表やヒストグラムから平均値と標準偏差を導き出す手法を知っておきましょう。
比較的簡単で、便利です。
ヒストブラムから平均値と標準偏差を求めよう
階級値を求めよう
今回のヒストグラムから統計量を求める上で重要な数字、それが階級値です。
階級値とは、簡単に言えば、ヒストグラムの級を代表する数値です。
今回は、各電気使用量における世帯数を表現した、以下のヒストグラムを例に考えてみましょう。
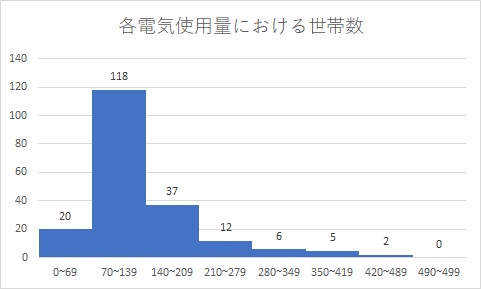
階級値とは、ここで言うと0~69(kWh)を代表する数字だったり、70~139(kWh)を代表する数字だったりします。
階級値は以下の式で導けます。
$$階級値=\frac{階級の端-階級の端}{2}$$
例えば、0～69(kWh)なら
$$階級値=\frac{69-0}{2}=34.5$$
例えば、70～139(kWh)なら
$$階級値=\frac{139-70}{2}=104.5$$
になります。
各級のど真ん中の数字を算出しているわけです。
それでは何故、級のど真ん中を代表値として算出するのでしょうか？
答えは単純で、級の中身が分からないからです。
そもそもヒストグラムとして集計すると、なぜ平均値などが算出出来ないかと言えば、級の詳細な中身が分からなくなるからです。
なので、何かしら代わりの値が必要なのです。
基本的にヒストグラムの級は、最頻値が真ん中に来るようにして級を作るように決められています。
つまり0～69の範囲における最頻値は34.5なのです。
0～69の級の内訳が分からないので、とりあえず最頻値である34.5を級の代表値として扱うという訳です。
ここを押さえればそれほど難しくはありません。
階級値を利用して平均値を求めよう
ここからヒストグラムに代わり、度数分布表を使って解説します。
その方が分かりやすいからです。
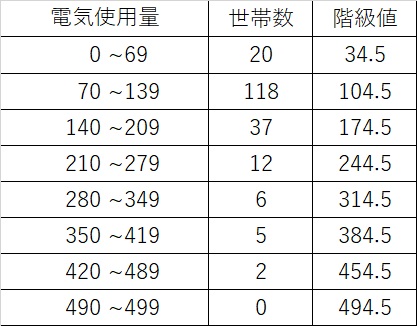
階級値まで、先ほどの公式で出した後、次は
$$階級値×度数(ここでいう世帯数)$$
を行います。階級値を何回足すのかをそれぞれ出すのです(加重平均と同じ道理です)
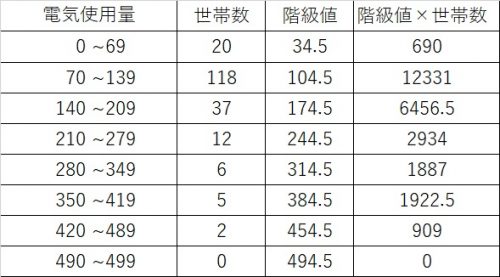
次に階級値×世帯数の総和を世帯数の総和で割ります。
$$平均値=\frac{\sum{(階級値×世帯数)}}{\sum{世帯数}}$$
計算すると、約135.7という数字になるはずです。
試してみて下さい
階級値から標準偏差を求めよう
次に標準偏差を求めます。
まずは、偏差を求めます。
各偏差は
$$偏差=階級値-平均値$$
です。
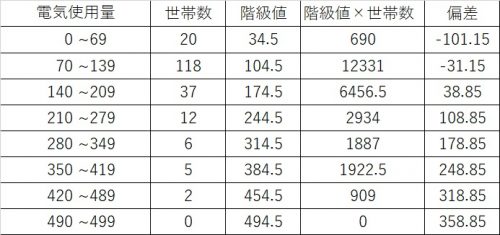
標準偏差では偏差を二乗してから平均値を求めていきます。
なので、偏差を二乗し、そこからは加重平均と同じ計算を実施します。
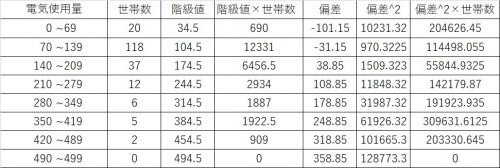
この偏差^2×世帯数を総和したものを、世帯数の総和で割れば、分散が算出出来ます。
この分散を平方根すると標準偏差になります。
約78.2という数値になるはずです。
計算してみて下さい。
また、注意点ですが、ここで求めた標準偏差は実際の標準偏差より小さくなります。
というのも、元の級には様々なデータが存在しているのに、階級値として一つの値しか使っていないからです。
級内変動を除外しているという事です。
なので、ヒストグラムで求めたばらつきは実際より小さくなるという事を肝において使用してください。
まとめ
世の中には、ヒストグラムを出しても平均値や標準偏差を出さない輩というモノが存在します。
それらの値が無ければ、予測も出来なくなるので、そんな場合は階級値を使って平均値や標準偏差を求めましょう。
平均値や標準偏差が求まるという事は、正規分布からの規格値の設定や、変動係数なんかも求まるという事ですから、ばらつきの比較も可能になります。
結構便利なテクニックなので、機会があれば使ってみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか？
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう
コメント
はじめまして。りおじーと申します。丁寧に解説していただいてありがとうございます。
一つ質問させていただいてよろしいでしょうか。
途中までの偏差の2乗かける世帯数までは理解できました。
そこから、世帯数(n)で割ると出てくるのはSD^2、つまり分散ではないでしょうか。
標準偏差を出すために、そこから分散の正の平方根を出す過程が必要ではないでしょうか。
教えていただければ幸いです。よろしくお願いします。
あっ本当だ。修正しますね。ありがとうございます。