統計における便利な手法に、検定があります。
通常データの比較をする際に、平均値を出して比較をしますが、その平均値の差が誤差によるものか、有意なものかは中々はっきりと判断が出来ないものです。
ですが、この検定を使えば、平均値などの統計量に有意差があるかをチェックする事が出来るのです。
チョー便利!
ですが、この手法にも注意点があります。
通常は3群以上のデータの比較が出来ないのです。
検定の多重性問題の為です。
ですが、やはり3群以上のデータを比較したいシチュエーションってのもあります(ていうか、そのシチュ数えきれない)。
その3群以上の検定を可能にした手法を総称して、多重比較法と呼びます。
この手法を使えば、t検定では出来なかった3群以上の比較をする事が出来るのです。
「よし、それではこの多重比較法を使えば敵なしだね!」
とは、ならないのが統計の世界の恐ろしいところでして。
という事で、今回は多重比較法の使用における注意点を紹介します。
多重比較の注意点

分散が等しくないと使えない
まず、多重比較法における注意点として、すべてのデータ間の分散が等しい事が挙げられます。
これは、多重比較法は各データのばらつきを合成したものを使用するからです。
例えばテューキー法の場合、
$$t=\frac{\overline{x_i}-\overline{x_j}}{\sqrt{V_E(\frac{1}{n_i}+\frac{1}{n_j})}}$$
ただし、
$$V_E=\sum_{i=1}^α{(n_i-1)V_i/φ_E}$$
ここでのVEは、一元配置分散分析の誤差分散に当たるものです。
この一つの分散値を元に検定を実施するので、各データのばらつきがバラバラだと、うまく機能しないのです。
ちなみに、2群の比較のt検定では、バラツキが異なっても機能するwelchのt検定というモノがありますが、
多重比較法では、それに該当するものが(私が現状知る限りでは)ありませんので、そこを注意する必要があります。
「じゃあ、どう気を付けるのさ」
って話なんですが、F検定は使うのは不適切でしょう。
F検定も2群の比較では、同様の理由(多重性問題)で機能しないので。
なので、ここは箱ひげ図で比較するのがベストでしょう。
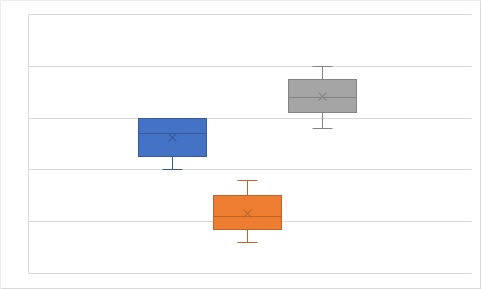
箱ひげ図の箱の部分は、四分位範囲と呼ばれる標準偏差みたいなバラツキの指標です。
この箱が画像のように、概ね同じサイズなら多重比較法を適用してもOKです。
目視確認になってはしまいますが、検定を使う訳にもいかないので、この辺りが無難な落としどころです。
箱ひげ図に関しては、こちらを参照ください。
分散分析と一緒に使わない方が良い
よく、様々なところで多重比較分析は
分散分析を実施して、有意差があった因子に対して、水準間に差があるかどうかをチェックするように使う
と紹介されます。
ですが、基本的には分散分析と併用しない方が良いです。
これも、繰り返しになりますが、検定の多重性が発生するためです。
分散分析もその中にF検定を使用しているので、アカンよって話なわけです。
そもそも、水準同士に差が有るかどうかを知りたいときには、分散分析なんてまどろっこしい事をせずに、多重比較法をやれば良いのです。
多重比較法で有意差が判明すれば、注目した因子が有意に決まってます。
逆に、分散分析をして因子に有意差が分かった後に、水準間に有意差があるかどうか知りたいって時には、要因効果図で見える化すれば良いのです。
要因効果図は以下の感じです。
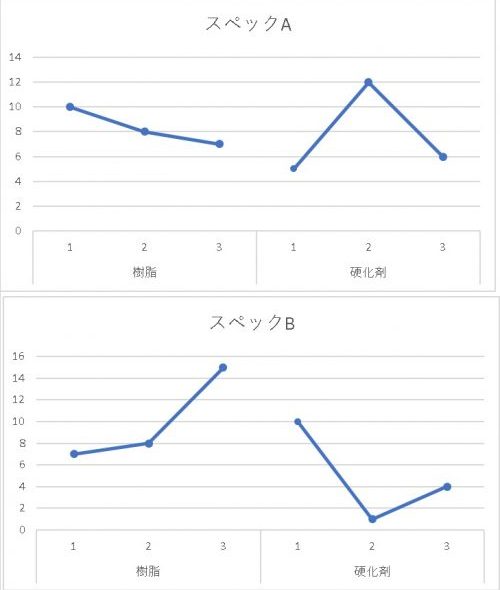
大抵、分散分析を使う場合と言うのは、水準間のそれぞれの有意差が知りたいという状況は稀です。
どちらかと言えば、最も効果的な水準一つだけが分かれば良い、というような状況の方が多いです。
なので、要因効果図で一番大きい(もしくは小さい)水準だけ発見出来れば良いのです。
以上の事から、分散分析と多重比較法は、併用できなくともそれほど問題は無いという事が言えます。
箱ひげ図と併用しよう
先程も申しましたが、多重比較法は箱ひげ図と併用した方が良いです。
箱ひげ図を使えば、平均、ばらつき、MAX-MIN、外れ値が全て把握かつ比較出来ます。
多重比較法が、ばらつきが全部同程度無ければならない、という縛りがある元でこの情報量は非常に便利です。
使い方としては、箱ひげ図でデータの概要を把握し、ダメ押しで多重比較法で分析というのが、シンプルかつ簡単かつ確実な分析法でしょう。
嬉しい事に、EZRで多重比較法での分析をすると、同時に箱ひげ図も描写されるので一発でこの分析が実施出来ます。
とても便利なので、ぜひ使ってみましょう。
まとめ
多重比較法は非常に便利ではありますが、注意点も多いです。
ですが、箱ひげ図と併用し、多重性の問題に気をつければ活用の場が非常に多い分析方法でもありますので、ぜひ活用してみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント
いつもYouTube楽しみに見てます。
以前の直交表実験すごく勉強になりました。
希望としては、多水準や分割実験についてもアップしてもらいたいです。
難しいと思いますが、よろしくお願い致します!