統計学の分析手法において、メジャーなものは悉くが正規分布を前提とした手法です。
という事は、分析対象とするデータが正規分布をしているのか否か。
これが非常に重要なわけです。
データが正規分布か否かを知るための分析を、正規性の分析と言ったりするのですが、今回はいくつかある正規性の分析の中の、尖度(せんど)と歪度(わいど)の検定について解説をしていきます。
いきなり尖度だ歪度だと言われても、何のことやらさっぱりという方も多いでしょう。
その辺のところも含めて解説していきますので、目くじら立てずに聞いていってくださいね。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
尖度と歪度とは?

正規分布を特徴づける代表値
通常正規分布の形状を決定づける因子として、解説されるのは平均値と標準偏差の2つです。
故に、統計的な分析において平均値と標準偏差の登場頻度が非常に多いわけです。
ですが、実のところこの2つの統計量とは別に正規分布を特徴づける値が存在します。
それが、尖度と歪度です。
正規分布を形成するときに、標準正規分布の尖度と歪度は一定の値を取ります。
故に、尖度と歪度の値がその一定の値と一致しているかどうかを検定する事で、正規分布であるか否かを確認することが出来るのです。
それでは、その尖度と歪度とは一体何を表す値なのでしょうか。
尖度とは?
尖度とは分布の尖り具合、もしくは裾野の伸び具合を示した数値です。

以下の数式で与えられます。
$$b_2=\frac{n\sum{(X-\overline{X})^4}}{[\sum{(X-\overline{X})^2}]^2}$$
実際にヒストグラムを書くとき、この尖り具合がどの程度であれば正規分布と言えるのか、見た目で判断することは難しいです。
なので尖度を計算して見える化し、正規分布である場合の尖度と比較することで正規性を検定することが出来ます。
先程の図でも書いてありますが、先ほどの式で計算すると正規分布の尖度は「3」になります
検定は
$$H0:b2=3$$
という尖度=3(つまり正規分布に等しいか)を帰無仮説として実施することになります。
まずb2をb2*に変換する必要があります。
$$b_2^*=\sqrt{\frac{(n+1)^2(n+3)(n+5)}{24n(n-2)(n-3)}}[b_2-\frac{3(n-1)}{n+3}]$$
このb2*に対して
$$b_2^*>u_{α/2}+\frac{\sqrt{6}}{\sqrt{n}}(u_{α/2}^2-1)$$
もしくは
$$b_2^*<-u_{α/2}+\frac{\sqrt{6}}{\sqrt{n}}(u_{α/2}^2-1)$$
となった場合、H0が棄却されて尖度≠3(つまり正規分布ではない)と検定されます。
ちなみに、uα/2は有意水準αのときの標準正規分布の上側100%α点です(有意水準α=5%の時は1.96)。
特に尖度は、線対称な分、一見すると正規分布に見えてしまいます。
そういう意味でも、正規分布かどうかを確認する際に尖度を検定出来れば、見た目に騙されなくて済むため、覚えておくと結構便利です。
歪度とは?
歪度とは分布が対称であるかを示す値です。
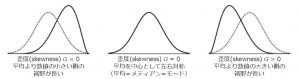
以下の式で与えられる数値になります。
$$\sqrt{b_1}=\frac{\sqrt{n}\sum{(X-\overline{X})^3}}{[\sum{(X-\overline{X})^2}]^{3/2}}$$
実際に採取したデータでヒストグラムを書くと、対称性が保たれていないことの方が多いです。
なんとなく、真ん中あたりが一番高くて、なんとなく均等に広がっているヒストグラムを見ると、
「あっ正規分布だ!」
と捉えてしまう事があると思うのですが、この歪度という観点からも、それがいかに危険かよく分かると思います。
完全な線対称のヒストグラムはまずありえないので、どの程度が今日範囲の歪みなのかは非常に重要なわけです。
歪度を使えば、どの程度許容可能か判断出来るわけです。
そして、正規分布の歪度は「0」です。
先ほど述べた対称性のズレというのは、無論同データから導き出せる平均値と標準偏差から作図される正規分布に対してのズレという意味です(正規分布はの形状は平均値と標準偏差で決定されます)。
データの正規性を歪度に注目して検定する場合は、
$$H0:\sqrt{b_1}=0$$
という歪度=0(正規分布に等しいか)を帰無仮説として実施することになります。
歪度による正規性の検定は、以下の式で行います。
$$|\sqrt{b_1}|>\sqrt{\frac{(n+1)^2(n+3)(n+5)}{24n(n-2)(n-3)}}[u_{α/2}+\frac{3}{2n}(u_{α/2}^3-3u_{α/2})]$$
uα/2は有意水準αのときの標準正規分布の上側100%α点です(有意水準α=5%の時は1.96)。
上式が成立した場合、H0帰無仮説を棄却します(つまり正規性は無いとなります)。
歪度の影響は特に片側検定の場合に、大きくなると言われています。
まとめ
正規分布の形は、平均値と標準偏差で決定づけられますが、分布を特徴づける値としては更に尖度と歪度が存在します。
ヒストグラムで正規性を目視判断しようとすると、必ずある程度尖ったり、歪んだりするので中々難しいものがあります。
なので、尖度と歪度での正規性の検定が出来るようになれば、そういったものに胡麻化される可能性が低くなります・・・が、
ここまで読んで頂いた方なら分かって頂けると思いますが、式がめっちゃ面倒くさいです。
私自身、正直に白状すると、これらの手法で正規性の検定を実施した事ありません。
Q-Qプロットとシャピロ-ウィルクの検定の方が、実用的で分析ツール的にも簡単です。
尖度と歪度は、「そんなものもあるんだな、気をつけよう」
くらいに捉えて、ぜひQ-Qプロットとシャピロ-ウィルクを使ってみて下さい。
便利ですよ。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ!」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます!!
買い切りタイプなのでお得です。
ぜひお求めくださいな。




コメント