開発やクレーム対応の対策の時、よく直面するのが
トレードオフの関係の両立
これです。
すなわち、
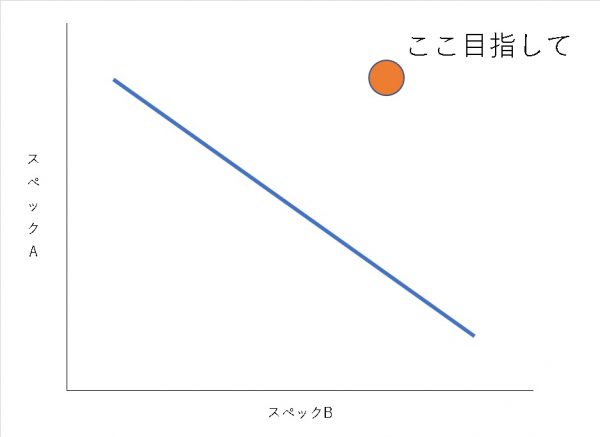
スペックAを上げると、Bが下がり、スペックBを上げるとAが下がるような関係性なのに、
両方上げて
という要求。
こんな話が来るたんびに、そんなの無理だよって会社を辞めたくなります。
このような状況に直面した場合、基本的にはスペックA,Bの間の丁度良いところに調整をしてしまいがち。
ですが、それでは他社に出し抜かれてしまいます。
少なくとも、あなたが勝者になる事は無くなります。
モノづくりをやっている限り、いつかはこの矛盾するような要求をクリアしなくてはなりません。
という事で、今回はスペックのトレードオフを乗り越える画期的な手法をご紹介いたします。
トレードオフの関係のスペックを同時に上げたい
矛盾を超える重要性
このような矛盾を乗り越える事って、一見すると無理に見えます。
ですが、顧客からすればそのような要求をするのは当然の事。
だってそれが無いと、お客さんが困ってしまうから。
これはまさしく需要なのです。
そして、企業というものは需要を満たす、つまりお客さんを助けるのが使命ですので、このような矛盾を無理だよと突っぱねるのは、存在意義を問われることになります。
それにあなたに難しいという事は、競合も難しいという事。
つまり、その問題を解決出来れば他社と差をつける事が出来るという事になるのです。
組み合わせ実験を繰り返しても・・・
このような開発を実施する際に、よく使われるのが直交表と分散分析です。
ですが、このトレードオフを相手取る場合問題点が発生します。
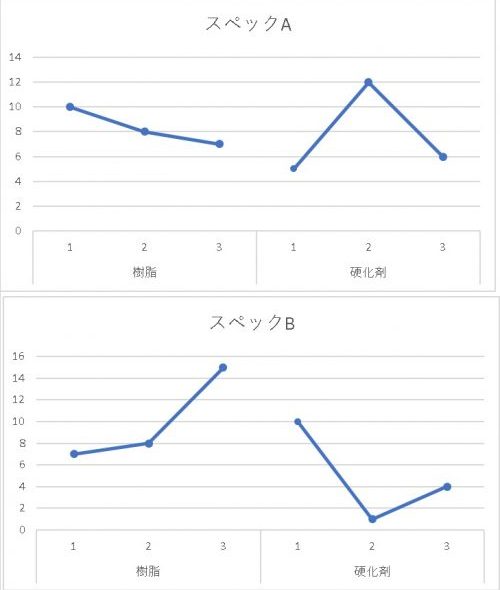
例えば上図のように、樹脂を1,2,3と振るとスペックAは低下し、スペックBは上昇します。
トレードオフなので当然です。つまり分散分析ではスペックAの最適な組み合わせとスペックBの最適な組み合わせは導けるのですが、スペックA,Bを同時に満たす組み合わせが分からないのです。
さて、困り果てました。
トレードオフを克服するための1軸評価
軸を回転させて評価軸を一つに
分散分析では、なぜトレードオフの評価でうまく機能しないのでしょうか。
それは、評価軸が2つ存在するからです。
分散分析は、目的変数yが一つの時に威力を発揮する手法です。
故にスペックA,Bのように2軸存在する場合、しかもそれがトレードオフの場合はうまく機能しないという訳です。
という事で、これをどう解決するか。答えは単純。
軸を一つにしてやることです。
以下のグラフを見て下さい。
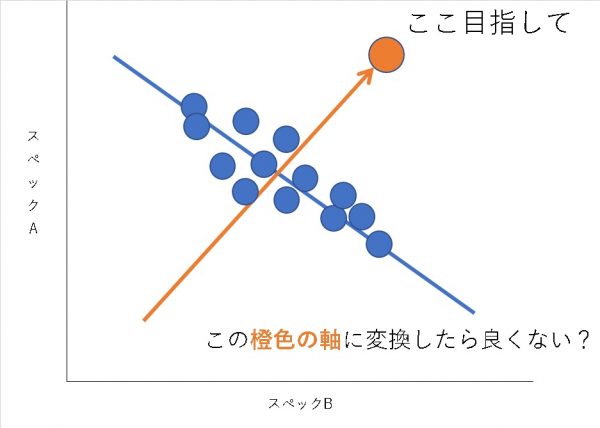
先程のグラフに加筆したものですが、要はスペックA,Bを上げるにはグラフの右上に行けば良いわけです。
つまりグラフの右上に向かう軸で評価をしてあげれば、スペックA,Bを両立出来る分散分析を実施出来るはずなのです。
それではどのようにしたら、軸を変換できるのでしょうか。
発想法としては、回転です。
以下のように軸を回転させれば良いのです。
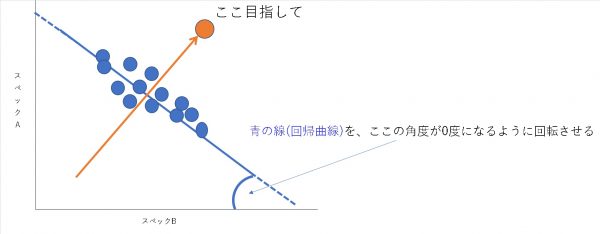
今回は、私が実践している軸の変換式をご紹介いたします。
軸の回転方法
まずは、エクセルの散布図でスペックA,Bに当たるようなトレードオフの関係グラフを描画しましょう。
次に回帰曲線を引きます。
今回の場合は、グラフが右肩下がり、つまりトレードオフの関係を対象にしていますので、基本的に先ほどのような青の実線みたいになると思います。
(トレードオフだが、数値の増減と性質の増減が合わない、例えばスペックAは数値高いと悪いがスペックBは数値低いと悪いみたいな場合は、片方を逆数にするとかして調整してください)
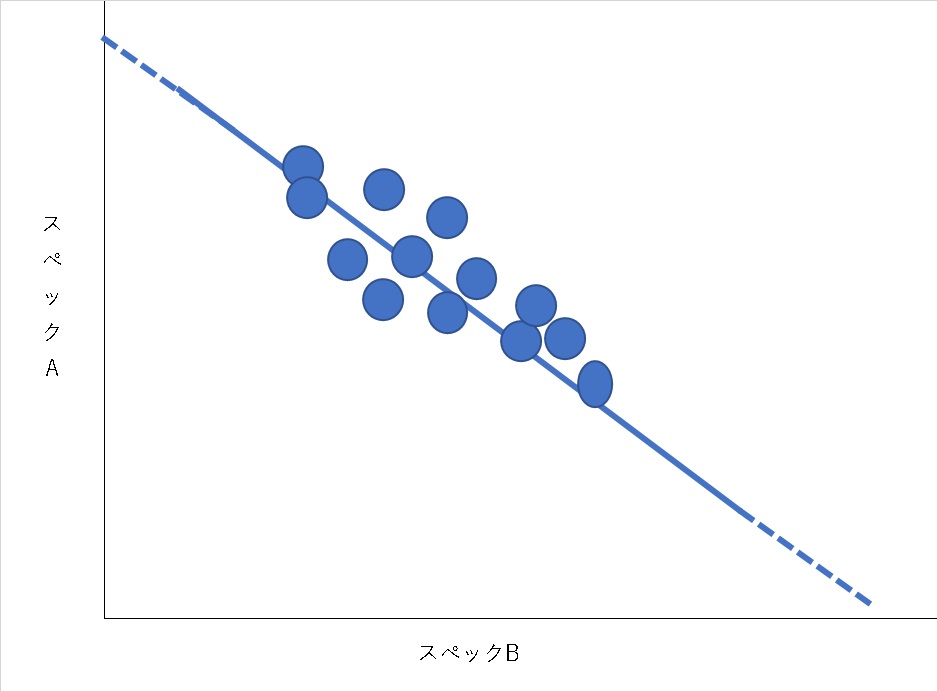
この直線はエクセルの近似曲線モードで自動で引けます。
更に近似曲線の「グラフに数式を表示する」で一次式を表示します(ちなみに今回はこの直線を基準に回転させるだけなので、決定係数は気にしなくて良いです)
そして、xが0の場合のy値とyが0の時のx値、すなわち
(0,y)と(x,0)
を導き出しましょう。それらの値を使ってタンジェントを使うと回転させる角度が算出出来ます。
以下の図のイメージです。
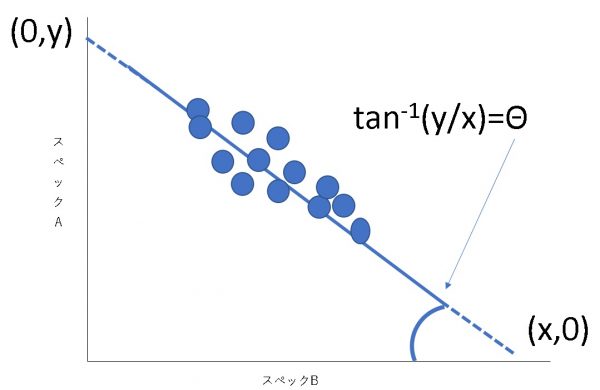
$$Θ=tan^{-1}(y/x)$$
次に算出したΘを使って各データのx,y値を以下の式で変換します。
$$Y=xsinΘ+ycosΘ$$
これで完了です。
このY値で分散分析を実施すればスペックA,B両方が向上する組み合わせを見出すことが出来るようになります。
実際に私はこの軸変換、直交表、分散分析を駆使して、右上にシフトさせる処方を見出しました。
凄く使える手法ですので、ぜひ使ってみて下さい。
まとめ
トレードオフの突破は、開発で付加価値を生み出すための必須事項です。
本来なら直交表と分散分析で最適な組み合わせを見出いしたいのですが、2軸だとうまく機能しません。
そこで導入すべきなのが、軸を回転させることで一軸に変換する事。
これを実施すると、直交表、分散分析でトレードオフを突破するための評価を実施する事が出来ます。
私自身、この方法で何度もトレードオフの関係を突破する組み合わせを見出しています。
ぜひ使ってみて下さい。
認められるビジネスパーソンの勉強方法とは?
おススメ記事




コメント
ちょっと数理的になるけれどダイセルイノベーションパークの首席技師で元島根大学客員教授の久保田邦親博士(工学)の材料物理数学再武装はトレードオフ工学を俯瞰できる品質工学と人工知能のあいのこみたいな講義資料結構面白いよ。博士のSNS覗いたらイギリスの古典派経済学の父アダムスミスの供給-需要曲線(神の見えざる手)を関数接合論で接合していていろいろと応用できそうな必読の情報だと思う。