仕事をする上で、業種に関わらず様々な実験を行います。
「自分の仕事は研究とかじゃないから関係ない」と言っているそこのアナタ!
実験とは理論や仮説が正しいかを立証する為に、要因を人為的に振って確かめる行為全般を指すのですから、
・経理ソフトの導入で効率性の変化を見る
・アンケートの結果からアクションすることで、売上の変化を見る
・採用プログラムを変える事で、新人/中途採用者の質の変化を見る
・教育プログラムを変える事で、部下の生産性の変化を見る
これらの行為も実験に当たります。
こういう視点で見ると、日々創造と解決に追われる社会人において実験という行為は切っても切り離せないものと言わざるを得ません。
そんな中、様々な要因を振っていると例えば個別ではイマイチでも、特定の組み合わせになると劇的に効果が上がる(もしくは下がる)という事、あったりしませんか?
このような作用を交互作用というのですが、実験においてこの交互作用が分かるようになれば、その交互作用は特別なノウハウになり得る筈です。
今回は、そんな交互作用を直交表による実験で知る方法を紹介いたします。
直交表と交互作用
直交表とは
直交表とは、最小の実験回数で効率的に効果のある要因を探り出すための組み合わせを示した表です。
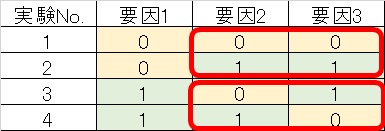
例えば要因1の効果を知るためには、実験No.1、2の平均値と実験No.3、4の平均値を比較すれば良いのですが、この際他の要因2、3については全ての条件が組み込まれているため、要因1だけに注目して観察出来るわけです。
詳細は以下の記事をご覧になってください。
交互作用とは
先述したように、特定の組み合わせにおいて効果が爆発的に上がる(下がる)ような作用の事です。
例えば植物の発育具合で
土:砂/粘土
水:硬水/軟水
でそれぞれ組み合わせて実験したところ、土の場合は粘土、水の場合は硬水を使った方が良かったとします。これをこのまま素直に受け取れば、粘土×硬水の組み合わせがベストマッチとなるはずですが、実は砂と軟水の組み合わせの場合だけ異常に発育がよく実はベストマッチだった・・・
これが交互作用です。
よく個別で食べると問題ないのに、食べ合わせると腹を壊すというものがあると聞きますが、あれも交互作用です(天ぷら×スイカとか)。
交互作用を知るためには?
交互作用を知るためには、総当たりで実験する方法もありますが、実は直交表を利用する事で知ることも出来ます。
実験回数を小さくしながら、交互作用も分かるのであればやらない手はありません!
交互作用を知るための割付方
直交表を用いて交互作用を知るためには、特定の割付方をする必要があります。
例えば22型直交表の場合は、
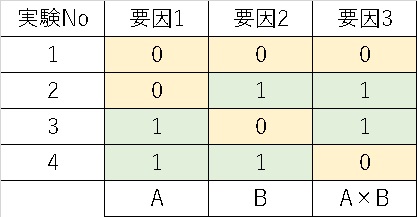
このように、要因1,2の交互作用は3列目の要因3の部分に該当します。例えば先の植物の発育について考えると、

こうなります。つまり交互作用を見たければ、実験No.1、4の平均と実験No,2、3の平均を比較すれば良いのです。
ちなみに、23型直交表の場合は
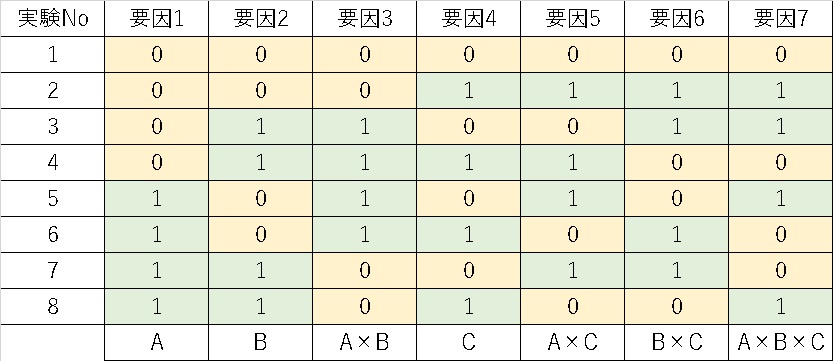
となります。要因1と2の交互作用は要因3に現れます。要因1と4の交互作用は要因5に、要因2と4の交互作用は要因6に現れ、要因1,2,4の交互作用は要因7に現れます。
間違って要因1,2,3に個別の要因を割りつけると交互作用が見れなくなって今います。
また、要因7のようにすべての交互作用が現れる欄があるのですが、通常3要因以上の交互作用は極めて小さいために誤差枠として用いられることが多いです。
このように、直交表によって交互作用の割付方は決められており、規則性はあるのですが基本的には非常に分かりづらくなっているのが実情です。
それではどうすれば、うまく割り付ける事が出来るのでしょうか?
線点図の使い方
直交表をネット上で検索しても、どうもイマイチ割付方が出てこないのが現状です。
割付方を知るためには、線点図と検索するとうまく出ます。
例えば23型直交表(L8)の場合は、こんな感じです。
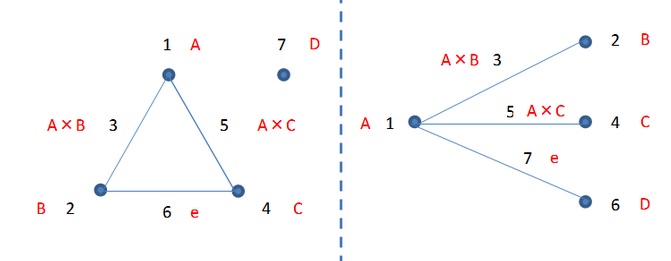
なんと2つ出てきました。そうなんです。実は一つの直交表で複数の割付方が存在します。
見方なんですが、点が独立した要因(土とか水とか)になります。そして点同士を結んだ線が交互作用になります。
左図の場合、1,2,4列目と7列目に独立した要因を配置します。
すると、
・3列目:1,2列目の交互作用
・5列目:1,4列目の交互作用
・6列目:誤差(小文字のeは誤差です)
という事を表しています。7列目に対応する交互作用は割付出来ません。
また右図の場合は、1,2,4,6列目に要因を割り付けると
・3列目:1,2列目の交互作用
・5列目:1,4列目の交互作用
・7列目:誤差
になります。左図や右図の誤差の項目ですが、これは誤差分析用に1項目取っておくという決まりごとのための処置であり、誤差と結果が混じっても良いのであればB,Cの交互作用としても構いません(交絡法)。
このように、直交表によって割付方は決まっています。しかも一つの直交表につき複数存在します。
この手の線点図や直交表は、実験計画法の本の索引に記載されているので、ぜひそれを活用してください。
まとめ
今回は交互作用について紹介しました。
直交表を利用する事で、交互作用を見る事が出来ますが、実は注意点もあります。
それは、あらかじめどこの交互作用に注目するか決めておく必要があるという点です。
やり方や直交表の種類によっては、交互作用の見れない要因も出てきます(L8の左図の7列目に要因を配した場合など)。
故に交互作用を見たい項目には、あらかじめ当たりをつけておき、考慮したうえで割り付ける必要があります。
また、実際のところ交互作用というものは、各要因単体の効果に比べれば限りなく小さい場合が多いです。
故におそらく無視可能と考えられる場合は、交互作用の列に別の独立した要因を割り付けた方が効率的になったりします。
こう聞くと運用は難しそうに聞こえます。
実際に私もはじめ、「なんかややこしくて、うまくいくかな?」と不安になりました。
ですが、やってみると意外と「結構使えるじゃん!」ってなります。
要はとりあえず使ってみる事です。
一度使って、再度調べると、気になっていたところが頭に入って来るようになります。
兎にも角にも、臆せず使ってみましょう。
道はそこから開かれます!





コメント