統計学には様々な手法が存在します。
検定、推定、正規分布を利用した管理図や工程能力指数
その中でも、回帰分析は過去のデータから未知のデータの予測が可能となる、非常に強力なツールです。
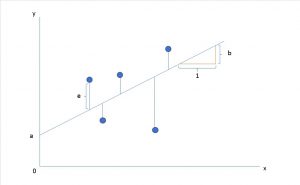
ですが、採取したサンプルから描かれた回帰直線は、サンプリングするたびに変化します。
当然ですよね?
サンプリングのたびに、平均値が振れるというのはおそらくアナタも経験があるはずです。
それと同じです。
ここで、重要になってくるのが、
「どのくらいの範囲で振れるのか?」
これですよ。
つまり、サンプルから得た回帰式の区間推定が出来れば良いわけです。
今回はそんな回帰分析の区間推定について、解説します。
回帰分析の区間推定

回帰分析とは?
まずは、おさらいついでに回帰分析の復習をしましょう。
回帰分析、特に今回扱う単回帰分析は、xとyの二変量の散布図を描いたときに、その関係性が直線関係を描くときの一次式を導きだすって奴です。

$$\overline{y}=ax+b$$
この回帰式が導き出されたら、まだデータとして得られていないxのy値を予測する事が可能となります。
導き方ですが、回帰式から導かれるyと個々のyの間の誤差が最小になるようにして導きます。
最小二乗法という方法を使って。
詳しくは、以下の記事を参照ください。
区間推定って何だっけ?
先程考えた回帰分析と言うのは、いったらピンポイントな式の予測です。
基本的には、サンプリングするたびにサンプルの数字は変わります。
つまり描かれる回帰直線も変わります。
なので、真の回帰直線はある一定の範囲にいるはずなのです。
こういう時に使う手法が、区間推定になります。
例えば平均値の区間推定の場合は(正規分布の時)、
$$-Z_{α/2}≦\frac{\overline{x}-μ}{σ/√n}≦Z_{α/2}$$
となるので、μつまり真の平均値を残す形で変形すると、
$$\overline{x}-Z_{α/2}σ/√n≦μ≦\overline{x}+Z_{α/2}σ/√n$$
とこんな感じになります。
つまり、真の平均値μはこの範囲内に存在しますよ~ってなる訳です。
これを回帰式に対しても出来れば、真の回帰式が少なくともどの範囲に存在するのかを知ることが出来るわけです。
回帰式の区間推定
回帰式の区間推定は以下になります。
$$ax+b±t(N-2,α)\sqrt{(\frac{1}{N}+\frac{(x-\overline{x})^2}{\sum{(x_i-\overline{x})^2}})V_e}$$
t(N-2,α)はN-2を自由度としたときの有意水準αのt値です。通常はα=95%になります。
Veは分散値です。
かなりややこしい式ですが、これは回帰式の係数、aとbのばらつきから導かれており、正直導出もかなり難しいです(私自身まだ完全に理解出来ていないです・・・)
ただ、使う分には、この通りに数字をぶち込んでやれば計算出来ます。
ちなみに、こちらのファイルに入っている回帰式のデータで、区間推定を行いました。
グラフだとこうなります。
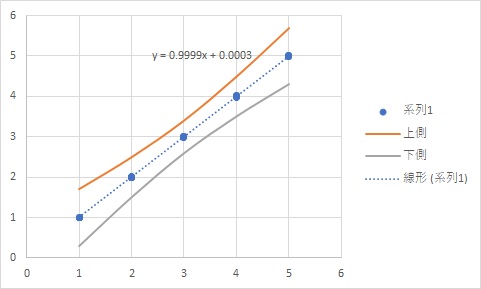
少し見づらいかもしれませんが、回帰式の中心から端に行くにしたがって、推定の範囲が広がっています。
散布したデータの中心の更に中央部分は、推定精度が高く、端に行くほど精度が落ちていく様を示しています。
基本的に、未知のデータを予測する場合は、それまでのデータの外(このグラフでいうと、0未満とか5より大きい値)を予測する事になりますし、外れれば外れるほど予測精度は下がるだろうなぁという事は、感覚的に理解頂けると思います。
この区間推定は、それをうまく表していますね。
今回は式の導出については、割愛しています。
理解出来たら、この記事を更新しようと思いますが、それでも待てへんという方は、こちらの記事を貼っておきます。
ぜひ、チャレンジしてみて下さい(そして分かったら教えて下さいな)
まとめ
回帰分析をしても、サンプリングごとにそのデータはばらつきます。
そこで知りたいのが、真の回帰直線はどの範囲に存在するのかという事です。
それを示唆する手法が、回帰分析の区間推定です。
式そのものや導出はとても難しいですが、活用する分には式にデータをぶち込むだけです。
エクセルで関数とかを入れた専用ファイルを作るなり、カスタム関数を作ったりすれば実用はそれほど難しくありません。
更に高いレベルの分析が可能になりますので、ぜひ使ってみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント