この世には、正規分布以外にも様々な分布があります。
その中でも正規分布と同じくらいに実用可能性がある分布が、ポアソン分布です。
以前にも簡単に触れていますが、今回は適用出来そうなシチュエーションや扱い方の詳細を紹介していきます。
ポアソン分布とは?
小さな確率、大きなn数
ポアソン分布は、離散型確率分布の一種で、二項分布を変形させた分布です。
$$P(x)=\frac{m^xe^{-m}}{x!}$$
分布は以下のような形となります。
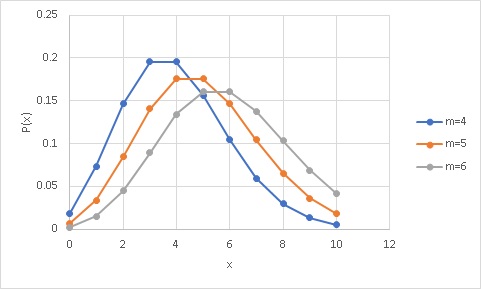
ポアソン分布はm=npの値で形状が決まります。またmは正の値しかとりません。
n数が極端に大きく、pの値が極端に小さい現象に対してよく当てはまります。
ポアソン分布表の活用
ポアソン分布は、m=npが分かっている状態で確率変数xの確率P(x)を算出することが出来ます。
しかし、実際に手計算をするには階乗や指数が絡んでいるため面倒です。
故に実際には以下のようなポアソン分布表を用いて確認します。
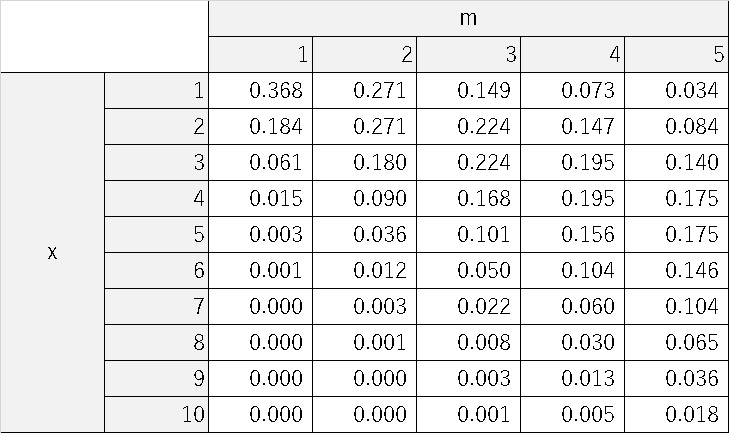
例えば、
『不良率2%の生産ラインで200個中6個の不良が発生する確率は?』
という場合に使うことが出来ます。
この場合
n=200、p=0.02、x=6になります。そして
$$m=np=0.02×200=4$$
になります。そしてポアソン分布表のm=4とx=6の交点に注目すると、
$$P(x)=0.104=10.4%$
つまり、この生産ラインで200個中6個の不良が発生する確率は10.4%と導き出せるという訳です。
エクセルによる算出法
先程一応分布表を紹介しましたが、実際には使うことはないと思います。
なぜなら、エクセルに関数が用意されているからです。
エクセル関数:=POISSON.DIST(x,m,FALSE)
カッコ内の末尾のFALSEは関数形式を指定するもので、分布表におけるx,mの交点の確率を算出します(TRUSEだと累積の確率を算出します)。
これを使えば一々分布表を引っ張り出す必要はありません。
どんな時に活用出来るの?
膨大な生産数 稀な観測数の不良
繰り返しますがポアソン分布は、nが大きくpが小さい状態でよく当てはまります。
このシチュエーションは、大量生産されている製造品に適用できます。
私が以前勤めていた半導体企業では、自動機による生産であったので、簡単に万単位、億単位の製品が流れていました。
そしてそのような大量生産ロットの場合、不良率は0.2%と極めて小さいものでしたが、生産数が多いので頻繁に観測されていました。
このように、現在の製造業においては機械で自動で作られるものが多く、正に
『膨大な生産数、稀な不良率、頻繁に観測される不良』
というシチュエーションが多いのです。
そのため1日で大量に生産する業界では、このポアソン分布はよく当てはまるのです。
平均と分散が一致するとき
以前にも紹介しましたが、ポアソン分布は平均値と分散値がともにmであり、一致します。
これは言い換えれば、平均値と分散を算出して値が極めて似通っていた場合、ポアソン分布をしている可能性があるということです。
目安のn数と不良率は?
ポアソン分布は二項分布の変形版です。
故に、二項分布とポアソン分布が一致し始めるnとpが見いだせれば、どの程度のnとpでポアソン分布を適用すべきか見えてきます。
まずn=12、p=1/3で考えます。この時に当然m=4になります。
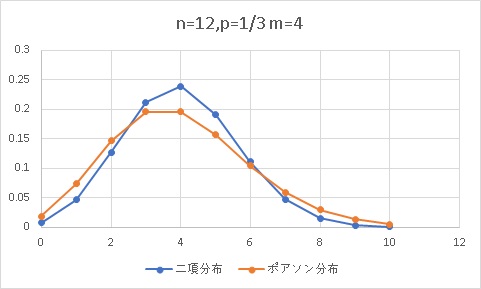
このくらいだと、どうもダメみたいです。
次にn=100、p=1/25で考えてみます。mは先ほどと同じく4になります。
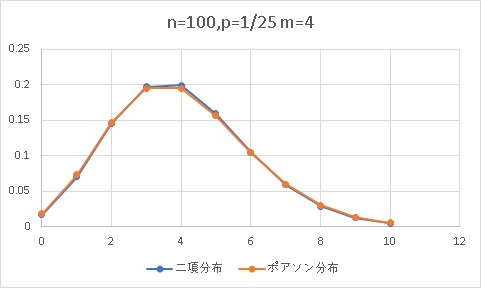
この時点でほとんど区別がつかなくなっています。
このように極端に大きなnと小さなpと言っても、実はこの程度の値なのです。
基本的にn≧100、p≧0.05程度でポアソン分布は二項分布によく一致すると言われています。
先程も述べましたが、製造業のラインではこれ以上のnとpが横行しています。
つまり活用する機会が多いという事です。
まとめ
今回はポアソン分布の内容と使い時を紹介しました。
この分布の使い時を知ることで、規格の決定や検定など、仕事における統計リテラシーをアップすることが出来ます。
ぜひ、自分の仕事周りでポアソン分布が無いか探してみてください。




コメント