統計学はばらつきの学問であり、その中で最も代表的な指標は標準偏差です。
正規分布を決定づける指標の一つなので、正規分布を中心とした様々な手法で活用されるためです。
しかしながら、標準偏差も万能ではありません。
実は弱点も多いので、なんでもかんでもばらつきを標準偏差で表現していると、痛い目に会ってしまいます。
今回は
・標準偏差の問題点
・標準偏差の代用となる数値
この2点について解説していきます。
動画でも紹介しています。
標準偏差の問題点

沢山のサンプルサイズが必要
まず、第一の問題点として、サンプルサイズが大量に必要と言う問題があります、
こちらの図をご覧くださいませませ。
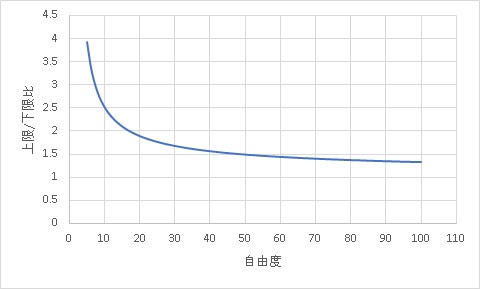
これは、標準偏差における自由度(N-1)とカイ二乗検定の上下限値の比の関係です。
すごくざっくり言うと、サンプルサイズの増大に伴う、標準偏差の精度を表した図です。
縦軸が小さくなると、精度が高いと言えます。
グラフを見てもらいますと、サンプルサイズがおよそ30ぐらいで精度がほぼ横ばいになってきています。
つまり、サンプルサイズN=30はないと標準偏差は精度が出ないと言えます。
詳細はこちらの記事を参照ください。
先程のグラフの成り立ちについても、きちんと解説していますので。
要するに、サンプルサイズが揃っていないと標準偏差は機能しないという事です。
もし、サンプルサイズが30を下回る場合は、標準偏差の使用は控えた方が良いです。
外れ値に弱い
第二の弱点として、外れ値に弱い点が挙げられます。
標準偏差は平たく言えば、偏差という値の平均値みたいなもんです(平方平均の平方根:RMSと言われる値)。
平均値は基本的に全ての値を足し合わせて、足した個数で割るので、極端に大きな値、小さな値が混入していると、その外れた値に引っ張られてしまうという特性があります。 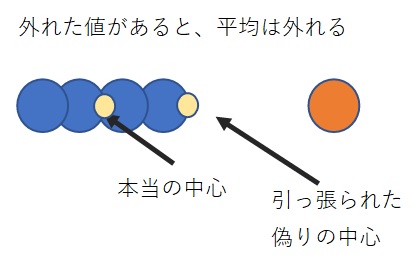
このあたりは、多くのサンプルサイズが必要と言う、先ほどの話ともつながってきます。
サンプルサイズが多いと、一つや二つの外れ値の影響が無視できるほど小さくなるためです。
なら、外れ値を外せばOKという話になりそうですが、どうやって外れ値と判断しましょうか?
一番基本的な外れ値の判断方法は、正規分布と仮定した上で、平均値±3×標準偏差から外れた値を除外するというモノです。
ですが、そもそも外れ値で歪んだ標準偏差を使って外れ値を外すなんて、話が堂々巡りしてしまってます。
当然正しく判断出来るわけがないのです。
このように、外れ値が存在していそうなときには標準偏差の使用を控えた方が良いです。
標準偏差の代わりの値 四分位偏差

四分位数とは?
このように標準偏差はいつでも扱えるという性質のものではありません。
しかしながら、サンプルサイズが小さい場合でもなんとかバラツキを表現したいというシチュエーションはよくあります。
その場合はどうするべきか。
実は以前、平均値の代わりに中央値を使うと外れ値の影響を受けにくい、というお話をさせて頂きました。
このバラツキの場合も、中央値のような値があればこの問題が解決出来るはずです。
さてそのような都合のいい値があるのか?
ありますよ。
四分位数を応用した、四分位偏差という指標を使えばOKです。
四分位偏差を理解する為に、まず四分位数を理解するのが肝要です。
四分位数とは、データの集団を小さい順(もしくは大きい順)に並べたときに、その集団を四分割にする値を指します。
以下のように、10個の値からなる集団を考えてみます。
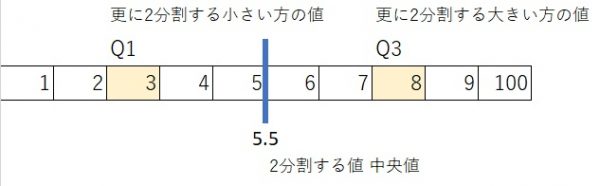
10個の値を2分割する値は5と6の間に当たる、5.5です。
これが中央値になります。
そして、1~5と6~100の2つの集団を更にそれぞれ2分割する値が
1~5の場合:3
6~100の場合:8
になります。
この小さい方の集団を2分割する値を、第一四分位数Q1と言います。
一方大きい方の集団を2分割する値を、第三四分位数Q3と言います。
これらの四分位数を利用してやることで、標準偏差に変わる値を算出することが出来ます。
四分位偏差について
四分位数である、Q3とQ1を用いて
$$IQR=Q3-Q1$$
で表されるIQRを四分位範囲と言います。
この値は、データのバラツキを表現します。
この四分位範囲を更に
$$四分位偏差=\frac{IQR}{2}$$
のように、2で割った値が四分位偏差になります。
Q3とQ1はいつでも、中央値に対して線対称の位置づけではないので、一度四分位範囲を出してから2等分してやるわけです。
先程の例で算出してみましょう。
Q1=3、Q3=8なので、
$$四分位偏差=\frac{Q3-Q1}{2}=\frac{8-3}{2}=2.5$$
となります。とても簡単でしょ?
ちなみに、データ量が膨大になった場合には、エクセルの
=QUARTILE.INC(データ範囲,0~4)
ただし、0:最小値、1:Q1、2:中央値、3:Q3、4:最大値
で簡単に算出出来ます。
四分位偏差の大きな特徴は、外れ値に強いという点です。
先程の図で示したように、1~9の集団に100が混ざっていましたが、中央値同様Q1とQ3もブレている様子がありません。
100の部分が、10でも、1000でも、1000000000であろうとも四分位偏差は全く同じ値のままです。
このように、四分位偏差を使えば外れ値に惑わされることなく、ばらつきを表現し、比較して利することが出来ます。
四分位偏差の欠点
このようにとても便利そうな四分位偏差ですが、当然こいつにも弱点があります。
それは、数学的に取り扱えないという事です。
つまり、標準偏差のように、分布の代表値とかではないので、確率的にどうこうと予測するのには活用出来ないのです。
四分位偏差で可能なのは、外れ値やサンプルサイズが小さい時の集団のばらつきの比較くらいです。
標準偏差の代わりに正規分布の代表値とかには、間違って使わないように注意しましょう。
まとめ
標準偏差は正規分布の指標の一つでもあるので、非常に活用範囲の広い値ではありますが、弱点もあります。
サンプルサイズが沢山いるのと、外れ値に弱いという点です。
これを回避して、ばらつきを表現、比較したい場合は四分位偏差を使いましょう。
中央値と同様、外れ値に強いという性質があります。
また、この四分位偏差を覚えておくと、箱ひげ図の理解も非常に早くなります。
データが足りない場面でも、正しい分析をするための武器として、扱えるようになりましょう。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント