前回複雑なものを単純な原因で表現する因子分析について解説しました。

ですが、折角の因子分析導き出した共通因子も、どの程度変量に影響を与えているかが分からなければ、当てにしていいのか不安になります。

夜も眠れません。

そこで今回は、算出した共通因子の共通性と寄与率について解説していきます。

因子分析の共通性

前回導いた式の中で、実は特に仕事をしなかったものがあります。

$$s_x^2=a^2+V(e_x)=1$$

$$s_y^2=b^2+V(e_y)=1$$

$$s_z^2=c^2+V(e_z)=1$$

今回は彼らに仕事をして頂きましょう。

前回の資料

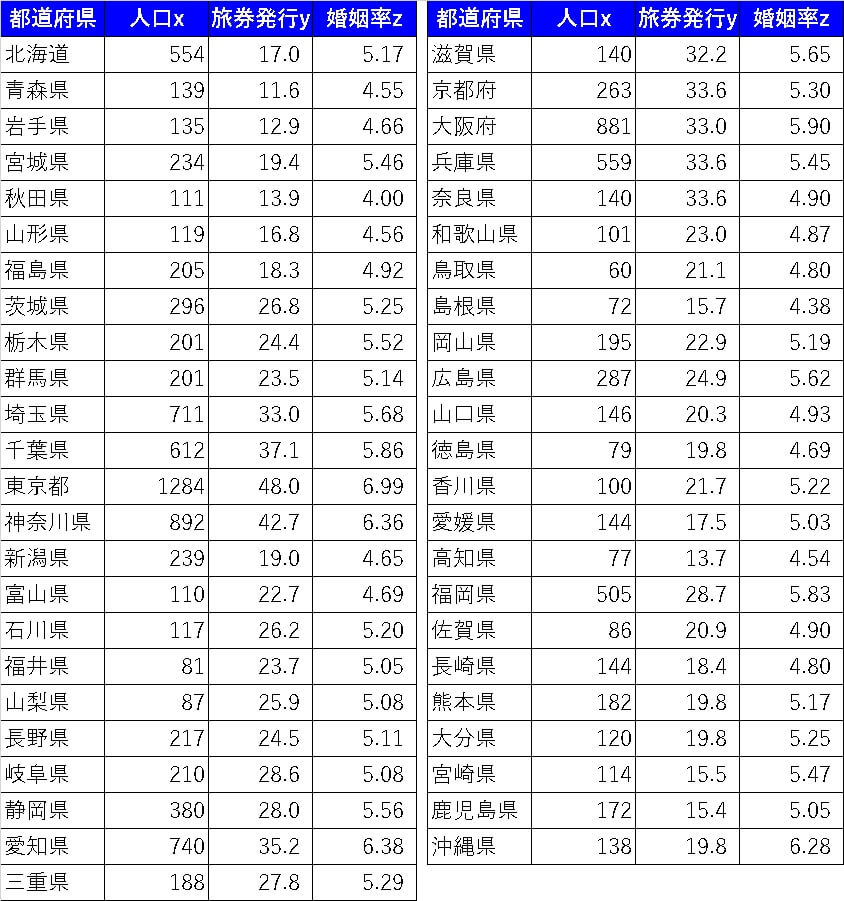
で導いた因子負荷量による回帰式は以下になります。

$$x=0.864F+e_x$$

$$y=0.856F+e_y$$

$$z=0.879F+e_z$$

この中でxだけについて考えてみます。

xの分散は先ほどのサボっていた3つの式の1つ目の式で表すことが出来ます。

$$s_x^2=a^2+V(e_x)=0.864^2+V(e_x)=0.764+V(e_x)=1$$

分散の加法性の性質から、分散は単純に足し算で積みあがっていきます。

つまり、総分散1の中の76.4%は共通因子で説明されるということを先の式は示しているのです。

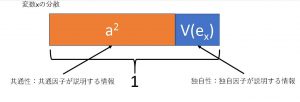
ここで共通因子で説明されるa²を共通性、独自因子で説明されるV(e_x)を独自性と呼びます。

ついてで、変量y,zの共通性も算出しましょう。

$$b^2=0.733$$

$$c^2=0.773$$

となります。

因子分析の寄与率

先程は各変量に対して共通因子がどのくらい値を説明しているかを調べました。

次に気になる事と言えば、共通因子が資料全体に対してどのくらい値を説明しているかです。

簡単に言えば足し算していきます。

まず各変量の分散を足し算します。これが資料全体の分散になります。

$$全分散量=s_x^2+s_y^2+s_z^2=1+1+1=3$$

続けて先ほど算出した共通性を足し算します。

$$因子Fが説明する分散の総和h^2=a^2+b^2+c^2=0.764+0.733+0.773=2.27$$

あとはh²を全分散量3で割れば

$$寄与率＝\frac{2.27}{3}=0.76$$

共通因子が資料全体に与えている影響寄与率が算出されました。

実はこの寄与率算出の発想は、以前紹介した主成分の寄与率の算出方法と全く同じです。

今回の内容でも分かる通り、分散の比率を用いることでどれだけ情報が組み込まれているかが分かるようになります。

この考え方は決して難しいものではありませんので、理解しどんどん使っていきましょう。