ある生徒が算数や理科の点数が悪い場合、おそらく

「この子は理系が苦手なんだろうな」

と連想するはずです。

更にその生徒が国語や英語の点数が良い場合

「この子は理系は苦手だけど、文系は得意なんだな」

と連想するはずです。

さてそうなると担任の先生は進路相談のときに、その生徒に対して文系の能力を活かす道を示すといったアクションをとることが出来そうです。

このように複雑な事象から単純な原因を、統計的に推測することが出来るなら、的確な説得力のある指導(つまりアクション)を取れそうだとは思いませんか。

この単純な原因を導き出す手法が、今回ご紹介する「因子分析」です。

因子分析のパス図

以前紹介したパス図で因子分析を見てみましょう。

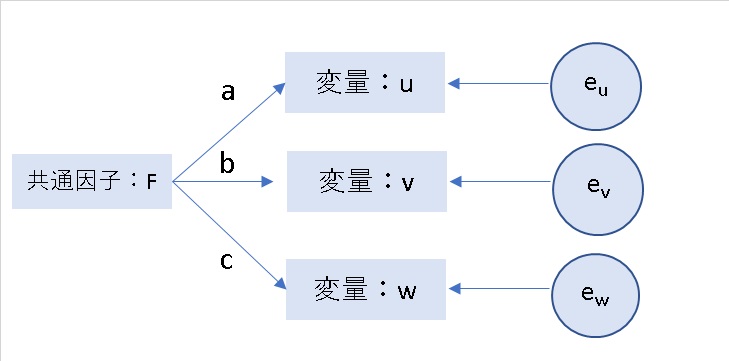
このように複数の変量を説明出来る共通の原因”共通因子“を導く手法が因子分析です。

先程の理系、文系の能力といった内容が共通因子に当たります。

また、因子分析では変量と共通因子以外に独立因子eも考慮に入れます。

共通因子で説明しきれない余った要素を独立因子とするのです。

ちなみに、このパス図のように共通因子１つでデータを説明するモデルを1因子モデルと言います。

当然共通因子を2つ、3つと考える場合もあります。

1因子モデルを考えてみよう

先程のパス図を式に起こすと以下のようになります。

$$x=aF+e_x$$

$$y=bF+e_y$$

$$z=cF+e_z$$

a,b,cは因子負荷量と呼ばれる量です。

ここからa,b,cを求めるには、これらの式から分散、共分散を求める必要があります。

多変量解析においては分散はそのデータが持つ情報量であり、主成分分析にしても因子分析にしても、データの持つ分散をどれだけ再現できる主成分、共通因子が導けるかがカギになるからです。

まずxに注目し、この分散を式で表すと

$$s_x^2=V(aF+e_x)=a^2V(F)+2aCov(F,e_x)+V(e_x)$$

Cov(F,e_x)はFとe_xの共分散という意味です。

次にx,yの共分散を式で表すと

$$s_{xy}^2=Cov(aF+e_x,bF+e_y)$$

$$=abV(F)+aCov(F,e_y)+bCov(e_x,F)+Cov(e_x,e_y)$$

となります。

「うわぁ、面倒くさそう」

と思ったあなた。

その感性、正しいです。

実際にこの式を解くことは非常に面倒くさいので、この式変形も式自体も特に覚えなくても良いです。

ここからいくつかの前提条件を加えることで、式が極めて簡単になります。

その１：共通因子と独立因子及び独立因子同士に相関はない

そもそも共通因子としてすべての共通項を抜け出した抜け殻が、独立因子です。

共通因子と独立因子間に相関がない(=0)と考えるのは至極当然のことです。

また独立因子同士も”独立”なのですから、相関性はないと考えることもこれまだ妥当と言えます。

つまり

$$Cov(F,e_x)=Cov(F,e_y)=Cov(F,e_z)=0$$

$$Cov(e_x,e_y)=Cov(e_y,e_z)=Cov(e_z,e_x)=0$$

です。これを取り入れると先ほどの式は

$$s_x^2=V(aF+e_x)=a^2V(F)+V(e_x)$$

$$s_{xy}^2=abV(F)+aCov(F,e_y)+bCov(e_x,F)+Cov(e_x,e_y)=abV(F)$$

となります。

その２：変量や因子を標準化する

標準化とは

$$u=\frac{x-\overline{x}}{s}$$

といった処理のことで、この処理をすると分散は1になります。

つまり

$$s_x^2=1$$

$$V(F)=1$$

とすることが出来ます。これを代入すると

$$a^2V(F)+V(e_x)=1$$

$$s_{xy}^2=ab$$

となります。かなりシンプルになりました。他の変量も並べてみましょう。

$$a^2+V(e_x)=1$$

$$b^2+V(e_y)=1$$

$$c^2+V(e_z)=1$$

$$s_xy=ab$$

$$s_yz=bc$$

$$s_zx=ca$$

この式を使えば1因子モデル因子分析は実行できます。今回実際に使用するのは下3つの式です。

実際に因子分析をしてみよう

それでは実際に因子分析をやってみましょう。

今回は各都道府県の人口x、旅券発行率y、婚姻率zの共通因子を探っていきます。

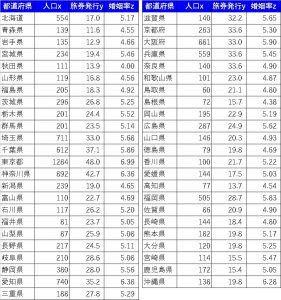
まずはこの値を標準化します。結果としては

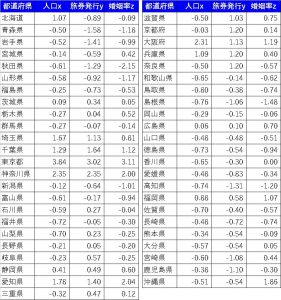
こんな感じになります。これらの各変量の分散は標準化しているので1です。

要(かなめ)は共分散になります(COVAR等エクセルの関数で簡単に求められます。)

$$s_xy=0.740$$

$$s_yz=0.745$$

$$s_zx=0.752$$

そしてこれらの共分散は先ほどの式から

$$s_xy=0.740=ab$$

$$s_yz=0.745=bc$$

$$s_zx=0.752=ca$$

このab,bc,caの式を解くと、a,b,cの値はそれぞれ

$$a=0.864$$

$$b=0.856$$

$$c=0.870$$

よって因子分析の式は

$$x=0.864F+e_x$$

$$y=0.856F+e_y$$

$$z=0.879F+e_z$$

となります。

この因子負荷量はデータが標準化されているために最大は1となります。

因子負荷量が大きいほど、共通因子が変量に与える影響が大きくなります。

つまり、a,b,cそれぞれが0.8を超えていることから、この共通因子は各変量に対してかなり大きな影響力を持っていると言えます。

この共通因子は一体何が考えられるでしょう。

共通因子が増えるほどに、人口が増え、旅券の発行率が上がり、婚姻率が増える。

例えるなら”地域の活性度”と言えるかもしれません。

地域が活性化するほどに、人口が増え、海外旅行者の数が増え、結婚している世帯が増える。

なんかそれっぽいですね。

以上が因子分析の流れになります。

因子や変量が増えたりすると、どんどんややこしくなる因子分析ですが、概念は決して難しいものではありません。

まずは、この手法が一体何をしたいものなのか。しっかりと捉えていきましょう！