こんにちわ、熊野コミチです。普段は製造業で開発をしながら仕事で使える統計学を解説する活動をやってます。
今回は標準偏差についてです。
標準偏差はデータのばらつきを表す統計学における代表的な指標です。
仕事でデータを扱う場合にばらつきという概念を考慮して、標準偏差を用いて分析出来るとその後のアクションの幅も広がります。
しかしながら、この標準偏差はなんにでも適用できる指標という訳ではありません。
こんな時は使わない方が良いというシチュエーションがあるのです。
今回は、そんな標準偏差を使わない方が良いシチュエーション3選とその対処法について解説いたします。
動画でも解説しています。
標準偏差を使わない方が良い場合

外れ値がある
標準偏差は二乗平均平方根(RMS)とされる値で、計算プロセスは平均値に似ています。つまり平均値と同様外れ値に非常に弱い性質を持っています。
例えば1,2,3,4,5,6,7,8,9,10
といった集団の標準偏差は約3.0です。
ここに100という値を加えてみます。
そうすると、約28.6という値になります。明らかに外れた100という値に標準偏差が引っ張られています。このように外れ値が存在していると不当にばらつきを多く見積もってしまいます。
この外れ値のせいで、不良ロットと誤判定するなどが起きてしまうとせっかくの良品を廃棄してしまうという事にもなりかねません。
標準偏差を算出する前に外れ値を適切に除外する必要があるのです。
サンプルサイズが少ない
サンプルサイズが少ないと標準偏差が正確に出ません。
一般的に必要なサンプルサイズはいくらかという所ですが、それに関しては下の図をご覧ください。
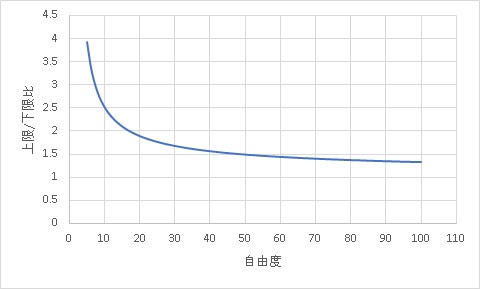
区間推定を利用して標準偏差が触れる幅がサンプルサイズに従ってどのくらい落ち着いてくるのかを示したグラフになります。
こちらを見ると、n=30以降から上下限の比がサチってきています(サチレーション=飽和)。
感覚的にはサンプルサイズが10でも様子見としては十分な感じではあるのですが、流石にn=5前後程度の場合はその標準偏差の値をあてにするのは厳しそうです。
量的変数じゃない
サンプルサイズが揃っており、外れ値が含まれていなくても量的変数出ない場合は標準偏差を使う事は出来ません。
数値は大きく分けて、質的変数と量的変数の2種類に大別できます。
質的変数で量的変数として誤用されがちなのが順序尺度で、その名が示すように順位で表現される数値です。
私は外観検査における不具合の程度を5段階に分けるといったものをよく見かけました。
一見すると数値として表現されているので平均とかしたくなるのですが、決してそのような処理をしてはいけません。
例えばマラソンの1位と3位の平均値は2位でしょうか。
なんとなく違うような気がしませんか?
このような計算が成立するためには、1,2,3の間隔が等間隔である必要があります。
ですがマラソンの1位と2位の間のタイム差と2位と3位のタイム差が均等とは限りません。
このように順位というのは平均の計算が成り立ちませんし、類似の計算過程をたどる標準偏差でも成り立ちません。
これを成立させるためには、マラソンの場合順位ではなくタイムを使う必要があります。
時間の間隔は等間隔(ちなみにタイムは比例尺度になります)なので、計算が成立するのです。
対応方法は?

基本的にはデータを取る前に、先ほどの例に当てはまらないかをチェックしてからデータを採取する必要があります。しかし既に測定してしまったデータに対してはなんかしらの対応をする必要があります。
それをこれから紹介していきます。
外れ値はIQRで判定して外そう
外れ値が入っているかどうかは、IQRを利用して確認し除外します。
IQRとは四分位数と呼ばれる数値を活用したばらつき指標です。詳細は以下。
箱ひげ図(ボックスプロット)って何? 分布を比較出来るグラフ
基本的には四分位数Q3+1.5IQRより上側に外れていたら、高めの外れ値
Q1-1.5IQRより下側に外れていたら低めの外れ値と判断されます。この方法の利点は分布の形状を問わない事です。
一般的には平均値±3σより外側というのが外れ値として紹介されますが、こちらが成立するのは正規分布になっているときだけです。しかもそもそも外れ値が入っていたらσの部分の標準偏差があてになりません。話が循環しちゃってます。
その点IQRによる外れ値判定はとても分かりやすく、状況を問わないし外れ値が存在していようといまいと判定がほぼ変わりません。
極端に条件を振って範囲を確認しよう
サンプルサイズが小さい場合は一旦標準偏差の算出はあきらめた方が良いです。
またロバストなばらつきの指標である四分位偏差もサンプルサイズが10未満の場合は見送ったほうが良いでしょう。
そんなサンプルサイズがどうしても確保出来ない場合は最大値-最小値である範囲を使う事になります。
ですが、単に範囲を使うだけでは本当のその値に意味があるのか疑わしいです。
そこで品質工学で用いられる誤差因子という発想を適用します。
データがばらつくのは様々な環境の違いが少しづつ影響を与えるからです。全くの同じシチュエーションで測定出来れば全く同じ値を返すはずです。
つまり、ばらつきの原因の中で、特に大きな影響を与えるものをわざと大きく振るのです。
強度を測る場合、厚みの違いでばらつくのであればわざと(ありえない範囲で)厚みを大きく振る。
厚みの変化に対応する強度の変化を絶った2点でも把握できれば、あり得る厚みの範囲でどの程度強度が触れるのかもおおよそ検討がつく。
こういった発想を適用することで、少ないサンプルサイズでもばらつきの情報を特定することが可能となります。
量的変数にするためには知恵を絞ろう
質的変数を量的変数にするには、その対象物に対する専門知識と知恵が必要になってきます。
とても先ほどまでに紹介した一般論で片づける事は難しいです。
ちょっと宣伝になって恐縮ではありますが、私がこれまで品質管理、製品開発において統計学を活用してきた経験から様々な現象を量的変数に適用する方法をこちらのnoteにまとめました。
もし今どうしても量的変数に置き換えるアイデアが浮かばない時には、ご参考ください。
それでも思い浮かばない場合は、お問い合わせ頂いても結構です。
ネタにもなるので大歓迎です。
まとめ
標準偏差はばらつきの指標としてもっとも代表的なものですが、いつでも扱える訳ではありません。
外れ値があったり、サンプルサイズが少なかったり、質的変数であったりするとうまく機能しないのです。
様々な対応法を紹介しましたが、一番大事なのはデータを取る前にこれらに該当しないかをチェックする事です。
このあたりに該当しなければ、他の統計学的手法にも適用出来ます。
ぜひ、注意してデータを採取してみてください。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント