交互作用というものがあります。
製品開発や何かしらの実験を行っている人は、ある程度真面目であればなんかしら効率よく実験出来ないか本屋なりネットなりをまさぐると思います。
そしてそんな方はかなりの確率で実験計画法や直交表といった単語に行き当たることでしょう。
そしてそれらの実験スキルでは、実験の工数減少の他に交互作用というものも分かるとされています。
この交互作用とは後でもうちょい説明しますが、ざっくりいうと組み合わせの妙みたいなもんです。
この交互作用というものが実験で分かると初めて知った人はおそらく
「すげぇ、この交互作用を使ったら普通に実験してて分からなかった凄い特性が見つかるかもしれねぇ」
と興奮することと思います。私はそうでした。
ちなみに製品開発における実験計画法や統計学の手法を解説した動画を公開していますので、体系的に学びたい方はコチラをどうぞ。
さてこの交互作用。実はそういった凄い特性を見つけるために使うものではありません。
実は表題にもあるように、クレーム対策のために活用すべき観点なんです。
今回はそんな交互作用との本当の付き合い方を解説します。
動画でも解説してます。
交互作用とは?

傾向が変わること
まず交互作用を簡単に解説します。
詳細な内容はコチラの記事をどうぞ
直交表で交互作用を解明しよう!【割付方の注意点】
先ほども述べましたが、組み合わせの妙の事です。特定の組み合わせをすると単独の因子では見られなかった傾向が表れる事です。
・塩はしょっぱく、スイカは甘い。組み合わせて食うと普通よりスイカが甘くなる。
・天ぷらとスイカ。単独で食うとうまいが同時に食うと腹をこわす(嘘という話もありますが)
こんな現象の事です。グラフで表現するとこんな感じです。
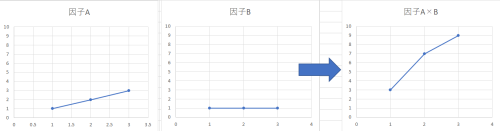
因子Aは若干右肩上がりの傾向で、因子Bはほとんど傾きがない。そんな2つを組み合わせたら普通は因子Aくらいの傾きしか得られないと考えられます。
しかしながら、組み合わせてみると想定外の傾きが得られる。これが交互作用です。
y値が高いほど高性能である場合、単独の因子では目標値に達しなかったのに組み合わせることでめちゃ高性能になったとなれば喜ばしい限りではありませんか?
そしてこの交互作用を確かめる手法があるとすれば、とても素晴らしい事だと思いませんか?
直交表を使えば交互作用が分かる
基本的に考えられる組み合わせすべてで実験して、グラフを書いて確認していけば交互作用を確かめることは可能です。
しかしながら、全組み合わせ実験というのはとても工数がかかるもの。普通やりゃしません。
4因子、3水準というパラメータ数は全然多いうちに入りませんが、実際にすべての組み合わせを実施するとなると、
34=81
という実験回数になります。嫌ですそんなの。なのでよく行われる実験は一因子実験です。
でもダメですからね。一因子実験は再現性が低くなりがちなので。
実験工数は減らしたいけど、再現性は確保したい。
ここで登場するのが直交表なわけです。
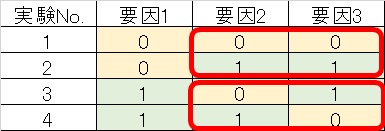
上の図はL4直交表というもので、3因子2水準という通常8回実施必要なところを4回で済ませられるよという組み合わせを示したものです。
秘密は各因子バックグラウンドが等しくなるようになっている点。
実験No.1,2は要因1は0という水準以外は要因2も3も水準0,1を含んでいる。
実験No.3,4も要因1は1という水準以外は要因2も3も水準0,1を含んでいる。
故に実験No.1,2の平均値と実験No.3,4の平均値を比較すると、要因1の水準0,1を比較することが出来る。
こういうからくりがあるんです。
若干話が逸れてきました。交互作用の話をしなければなりません。
直交表では交互作用を調べることが出来ます。
例えば先のL4直交表では、要因3の列に何も割り付けない場合水準0と1の平均値を分析すると(分散分析)要因1と2の交互作用の有無を確認することが出来ます。
故に直交表を使うことで全組み合わせで実験しなくても、交互作用の有無を確認することが出来ます。
交互作用がどの列に出るのかは、直交表によって異なりますがそれは線点図を使うことで確認することが出来ます。
設計における交互作用

性能を上げるために交互作用を使うな!
本題です。
交互作用を使えば、単純な一因子実験では見つけることが出来ない尖った特性を出せる組み合わせを見出せるかもしれません。
しかし交互作用で性能を上げようとするのはやめましょう。
ダメ、絶対
理由なんですが、それは再現性が出づらいからです。
そもそも交互作用というものは、特定の組み合わせで発現するものです。
その特定の組み合わせが曲者でして、要は絶妙なバランスで成り立っているとも言える。
そして交互作用を見つけるときというのは実験室での事のはずです(直交表でも実験数が多いので現場じゃムリ)。
交互作用が発現するのはあくまでその実験室の環境での話。
実験室から現場へ量産移管するときに、条件が違いすぎて期待していた交互作用が発現しないという事がしょっちゅうなんです。
実験環境の違い。これがほんとえらいもんでして。
主効果ですら再現性が低いので、傾向の動き方だけ把握して現場で微調整するのがセオリーです。
交互作用なんて出たらラッキーですが、ちょっとした環境変化でふらつく。
現場で作るのがとても難しくなること請け合いです(管理幅が狭くなる)。
そもそも工業製品というものは、再現性がとても大事。
ばらつきが尊ばれるのは職人の作品だけです。
交互作用で性能を出すというのは、ある種工業製品のありようと矛盾するものなのです。
クレームは交互作用で起きる
それじゃ交互作用って全然活用出来ないの?
いえ、そんなことぁありません。
再現性が成立しづらい交互作用ではありますが、重要な使い道があります。
たまにしか発生せず、それでもなお知りたい情報。
それはクレームの発生シチュエーションです。ちょっと事例で解説します。
例えばLEDの検査で
・LED内の電気を通すワイヤーの接合強度が規格の下限値ギリギリ(でも合格)
・抜き取りサンプルを加熱して異常が無いかを確認する⇒合格
・同じロットからサンプルを抜き取り振動試験にかける⇒合格
問題ないので出荷したら、お客さんのところでそのロットで点灯しないLEDが大量に発生した。
なして?合格してたのに。
その後検証した結果、
・LED内部の電気を通すワイヤーの接合強度がいつもより若干低かった(合格ライン)
・搬送時のトラックの内部が猛暑日かつ特に温度管理されていなかったのでとても熱かった(いつもの加熱試験よりは低い温度)
・トラックの搬送経路は舗装状態が悪い箇所があり、若干の振動がある(振動試験よりは緩い)
ちょっと過酷ではあるが、単独では検査で実施している条件よりは緩い。しかしながらそれぞれが組み合わさって
・熱で若干接合強度が落ちる。
・接合強度が落ちたところに振動が加わる
・いつもより若干低い接合強度で熱+振動に同時に晒されることでワイヤーが外れた。
という理由でクレームに発展しましたとさ。
どうでしょうか。クレーム対応したことがあるならば、あるあると頷いて頂けるものと思います。
クレームというのは、それはそれは様々なシチュエーションで発生します。
製品が出来てから時間が経つと単純な条件で発生するクレームは激減します。
大体初期ロットで発生して対策が打たれるからです。
厄介なのが事例のような複数の要因が絡まって発生するクレームです。
一見すると単一の特性値は管理値内なのに、複数の特性値が特定の値の組み合わせになると発生する。
そもそも再現が難しいので原因を特定するのも困難です。
さて、このクレームを未然に防止する為にはどう検証したらいいのか?
そこで交互作用です。
交互作用は、このような再現性が低いシチュエーションを調べるのにもってこいなんです。
つまり先ほどの事例では、因子にそれぞれ
・熱
・振動
を割り振って強度を測定すればよい。
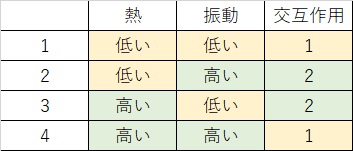
この検証をすれば、熱と振動が高い組み合わせの場合想定以上に強度が激減する現象が観測されるはずです。
これを発展させれば、お客さんが使用される環境を因子として割り振って主効果、交互作用を確認すればあらかじめどのようなクレームが発生しそうか確認出来ます。
この手法は品質工学では誤差因子の調合として活用されるものです。
交互作用は再現性が欲しいところで使うのではなく、再現してほしくない現象に使うべきものなんです。
まとめ
交互作用は尖った特性を出すために使うものと誤解されがちです。
ですが、再現性が低いため実験室⇒量産ラインと拡大する際に特性が出せなくなることが多い。
なので新しい特性を作りこむには向いていない。
では使えないのかといえばさにあらず。
クレームのあぶり出しでは非常に効果を発揮します。
クレームは万が一にも発生してほしくありません。
なので実験室段階でクレームが発生しうるシチュエーションを把握し、潰しこみが出来ていればこれほどありがたいことは無い。
交互作用は再現性が出にくいので、もしかしたら杞憂なクレーム現象もあるでしょう。実験段階で仕事が不必要に増えるかもしれない。
しかしながら、開発という行為は後ろに行くほど(実験室⇒量産⇒顧客)不具合時の修正コストが膨大になります。
故に実験室レベルでクレームが大量に想定できるという事は価値があります。
FMEAでも未然防止活動は出来るかもしれませんが、正直人の頭で考えつくクレームはたかが知れている。
直交表で組み合わせることで、こんな組み合わせは無いだろうというシチュエーションも検証出来る。そしてそんなところにクレームの種は潜んでいる。
ぜひ皆さんも面倒がらず、交互作用でクレームを芽吹く前に狩り切りましょう。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント