以前分析対象が正規分布であるか否かを判定する方法を紹介しました。
「さて、このQ-Qプロットでどうも対象とするデータは正規分布ではないことが分かった。」
「あれ?じゃあ統計的な分析は無理?差の検定とかも出来ないの?」
と思われる方もいるでしょう。
ご安心ください。統計学には決まった分布を取っていないデータを分析する手法が準備されています。
ノンパラメトリック分析と呼称される分析群です。
今回は個々のノンパラメトリック分析ではなく、そもそも分布を成していないのに分析出来るメカニズムを解説します。
これを押さえておくことで、個々のノンパラメトリック分析を学習する際理解しやすくなると思います。
統計的分析の前提
規則性がとても大事
統計的な分析をする上で、最も大事なことは規則性です。
分析対象の中から規則性を見出し、その規則性を利用して
「この規則性なら、このようなxを取る時にこのようなyになるはずだ」
という予測が出来るようになります。
そしてこの世界では、基本的に正規分布的性質を見せるものが多いために統計学では正規分布が多用されるのです。
当然、正規分布がダメでも、一様分布、二項分布、ポアソン分布のような規則性が見いだせれば分析することが出来ます。
このような特定の規則性(=分布)を利用した分析をパラメトリック分析と言います。
規則性が見いだせない場合は?
しかし、いつでも規則性があるとは限りません。
本当にランダムな場合もあれば、サンプルサイズが少なくて規則性が見いだせないものもあるでしょう。
このような場合、どうすれば良いのか?
統計学はこの難題に対して
『規則性がある数字に変換してやる』
という発想で乗り切りました。
これだと一見すると、「そんな無理矢理な事して、本当に当てになるのか?」という疑問が当然湧いてくると思います。
しかし、これから紹介する内容を聞けば、
「はぁなるほどなぁ」
という感想に変わると思います。
ノンパラメトリック分析
順位で考える
ノンパラメトリック分析では、規則性が見いだせない数字群をある規則性のある数字群に変換します。
それは順位です。
順位付けは
・もっとも小さい数は1
・もっとも大きな数はサンプルサイズに一致する
・数字は必ず1ずつ大きくなる
という性質(規則性)で成り立っています。
例えば、![]() このようなデタラメな数字群を順位に変換してみましょう。
このようなデタラメな数字群を順位に変換してみましょう。
まずは、大きさの順番に並び替えます。

そして、小さいものから順位をつけていきます。

ここで、同順位のものが2つ出てきました。この場合の対処法は決まっていて中間順位(別称平均順位)に置き換えます。
この場合は、
$$\frac{6+7}{2}=6.5$$
です。分母は同順位の個数であり、例えば6,7,8番目の数字がすべて同じ場合は
$$\frac{6+7+8}{3}=7$$
になります。
結果として、中間順位に変換すると
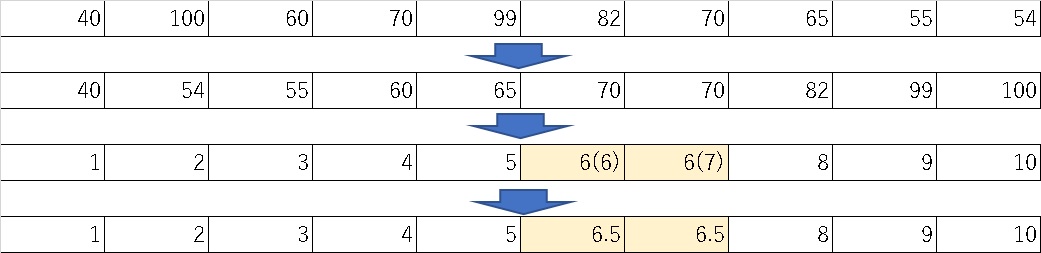
というようになります。これが順位の置き換えです。
このような順位に置き換えるメリットは繰り返しなりますが、規則性が出てくるということです。
サンプルサイズによって、平均値や分散に相当する代表値の期待値が決まってきます。
期待値とのズレを見極める事で検定を実施することが出来るのです。
どのように検定を実施するのか?
差の検定を行う場合、2群以上が存在する場合が多いです。
ノンパラメトリック分析では、2群の数字を混ぜ合わせて順位付けをして、本来のサンプルサイズによる期待値とのズレを分析します。
実際に見てみましょう。
以下のような2つの群を考えてみます。ブレンドしながら考えるので分かりやすいように色別にしています。
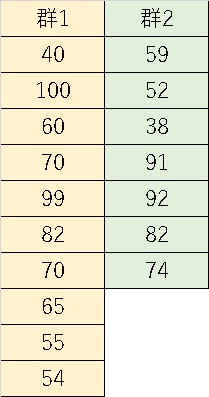
ここで、まずこの2群を混ぜて大きい順に入れ替えてみます。
![]()
次に順位をつけていきます。

ここで、同順位が2つあるので、それぞれを中間順位に置き換えます。

さて、ここで元の2群に分けてみましょう。
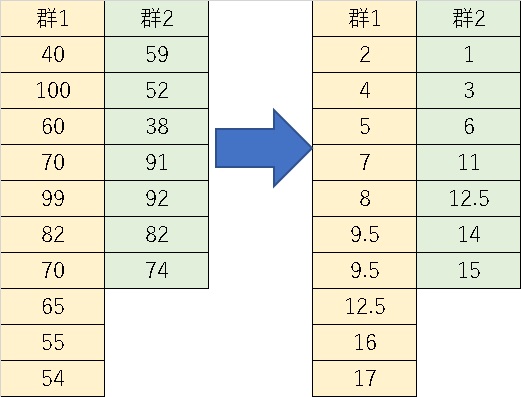
これが2群の場合の順位分けの方法です。
ここで、順位には規則性があるのですが、今回は順位の総和だけ触れておきます。
ある集団からn個だけ数字を取り出した場合、n個の和は
$$順位の総和の期待値=\frac{n_1(n_1+n_2+1)}{2}$$
になります。今回の例の場合群1はn1=10、群2はn2=7です。よってそれぞれの総和の期待値は
$$群1の総和の期待値=\frac{10(10+7+1)}{2}=90$$
$$群2の総和の期待値=\frac{7(10+7+1)}{2}=63$$
になります。そして実際の各群の総和は
$$群1の総和=91$$
$$群2の総和=63$$
になります。期待値と実際の値がほぼ同等であり、おそらく検定を実施すれば有意差なしと判定されるでしょう。
このようにして順位に変換すると必要な代表値の期待値が算出されますので、その期待値との差を見る事で分析を実施することが出来るようになるのです。
ノンパラメトリック分析の利点
ノンパラメトリック分析には、いくつかの利点があります。
まずは、正規分布でなくても分析が出来るということです。また正規分布であっても、多少検出力が低下しますが、適用することが出来ます。
最悪正規分布か分からない場合は、ノンパラメトリック分析を実施することが可能です。
また間隔尺度だけでなく、順位尺度にも適用可能です。
例えば検査で傷の度合いから1~5の5段階評価をしている場合、通常の正規分布を前提とした分析は当然適用出来ません。
しかしながら、ノンパラメトリック分析は分析過程で順位に置き換えますので、順序関係さえ分かっていれば分析することが可能です。
これは大きな利点です。
検査員の実力判定や、アンケートの評価分析にも適用することが可能であり、応用の幅は非常に広いと言えます。
まとめ
今回はノンパラメトリック分析の考え方について紹介しました。
一見規則性が見いだせない数字群も順位に適用することで、統計的な分析が可能となります。
また、これらの分析手法はEZRにも搭載されていますので、原理さえ押さえておけば、実際の計算はソフトに任せてしまってもよいでしょう。
今後は個々のノンパラメトリック分析についても紹介していきたいと思っています。




コメント