通常のt検定では、3群以上の平均値の差について有意差の有無を確認することが出来ません。
なぜなら、多重性の問題が存在するためです。
しかし、実際のところ3つ以上の平均値に関して、有意差が知りたいというシチュエーションは多いハズ。
この悩みを解消する手法が多重比較法です。
今回はそんな多重比較の中の一つダネット法について紹介いたします。
ダネット法とは?
対象群に対する差の検定をする多重比較法
以前紹介したテューキー法とは異なり、ダネット法は対象の群に対して検定する際に用いられます。
例えば群A1,A2,A3,A4,A5が存在する場合、テューキー法では
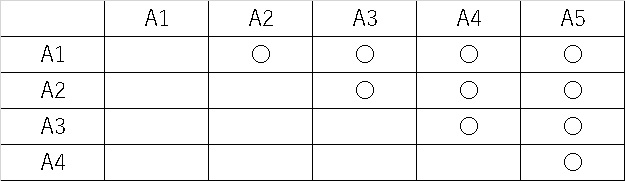
でしたが、対してダネット法では、
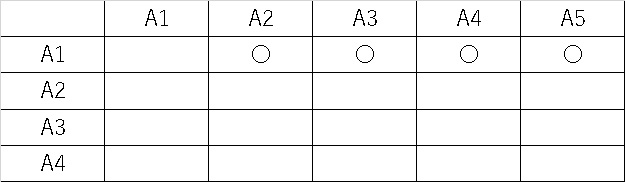
といったように、一つの群に対してそれぞれ検定を行うときに向いています。
基準となるリファレンスに対して、それぞれ準備したサンプルがどのような位置づけにあるかを検討する場合に使うと効果的です。
t検定との式の違い
実は検定統計量tを算出する式は、テューキー法と同じです。
$$t=\frac{x_1-x_2}{\sqrt{V_E(\frac{1}{n_1}+\frac{1}{n_2}})}$$
異なるのは、使用する標本分布です。
基本的に
$$ρ=\frac{n_i}{n_1+n_i}$$
で決定されるρによって使用する分布表が決まり、そこから有意水準αと誤差自由度φEで棄却域が決定します。
テューキー法の時にも言及しましたが、多重比較法を道具として扱う場合にはあまり厳密に原理を知る必要はないように思います。
一般的な統計知識の範囲を、明らかに超えているからです。
どうしても気になる方は、以下の本をお勧めします。
 | 新品価格 |
多重比較法について網羅的に記述されており、日本で多重比較を解説している数少ない本です。
EZRで実施してみよう
実際に分析してみよう
EZRにはダネット法も搭載されています。
今回もテューキー法の時に使用した、以下のような複数の群について分析してみましょう。

こちらも、実際にEZRに読み込ませる場合は縦に並べてください。
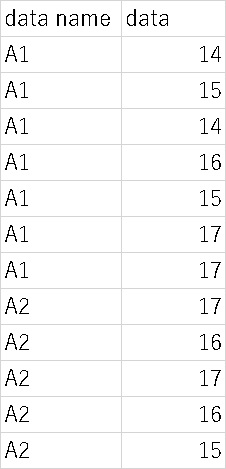
データをEZRに入力した後、『3群以上の平均値の比較』を選んでください。
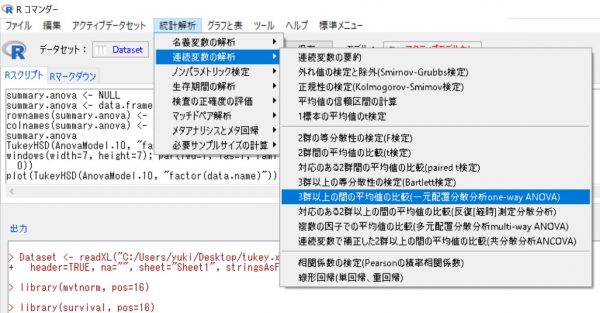
こちらを選択した後、
・比較する群には、データの名前を入れている行を選択してください。
・等分散と考えますかには、はいを選択してください(重要)。
・そして2群ずつの比較(Dunnett法)を選択してください。
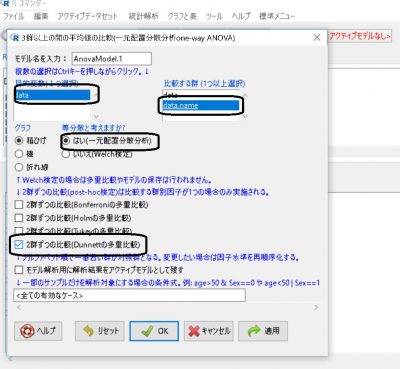
そしてOKを押せば結果が出力されます。
分析結果の見方
結果を見てみましょう。
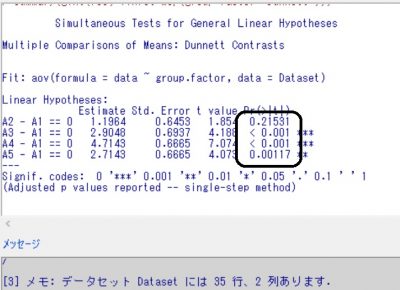
枠で囲んだPrの値が0.05よりも小さければ、有意差ありとして棄却されます。
この場合、A1に対してA3,A4,A5は有意差ありと判定されてました。
ダネット法の注意点について
テューキー法の時にも開設しましたが、ダネット法も前提条件として複数の群の全ての分散(つまり”ばらつき”)が等しい必要があります。
先述した式を見て頂ければ、その原因が分かります。
$$t=\frac{x_1-x_2}{\sqrt{V_E(\frac{1}{n_1}+\frac{1}{n_2}})}$$
分母には誤差分散しかありません。
welchのt検定では分散が異なるシチュエーションに対応する為に、分母には各群のσが組み込まれていますが、ダネット法では、この分散の値が一つだけなのです。
これを考慮して、EZRでのダネット法では、等分散と考えますかをいいえにすると、ダネット法が算出されません。
この点だけは注意してください。
まとめ
ダネット法を用いる事で、複数の平均値を同時に検定することが出来ます。
EZRを使用することで簡単に実施出来ますので、ぜひ皆さん活用してみて下さい。
あとがき
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント