t検定において最適なサンプルサイズを決めるためには、効果量Δを決める必要があります。
$$Δ=\frac{μ-μ_0}{σ}$$
ここで検定の設計者はどのくらいの平均の差μ-μ0を許容出来るのか、それを決定しなければなりません。
そして、標準偏差σはそれまでの測定経験から妥当な値を決定します。
以前も解説を投稿しましたが、効果量やそれとのサンプルサイズの関係について自分としても分かりづらいものがあったので、再度考えてみたいと思います。
今回はこちらの本を参考にしています。
サンプルサイズと検出力、効果量についての書籍というのは非常に少なく、貴重な一冊になります。
ぜひご一読ください。
効果量の意図するもの
効果量の式の構成は、「1σに対して、母集団の分布平均と対立仮説で成り立つ分布の平均の差がどれだけ開いているか」を示しています。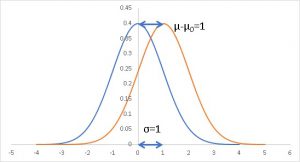
このグラフのように、σ=1に対して平均値の差も1離れてる場合が効果量1です。
そしてこの効果量からt検定においてのサンプルサイズを算出する式は
$$n=[\frac{Z_{α/2}-Z_{1-β}}{Δ_0}]^2+\frac{Z_{α/2}^2}{2}$$
です。有意水準α=0.05、検出力1-β=0.8と置いた場合、効果量1での必要なサンプルサイズは
$$n=[\frac{1.96–0.82}{1}]^2+1.92=9.8$$
とn=10程度ということになります。
この状態(つまりn=10)で帰無仮説が棄却されなかった場合
「平均値の差がもしあったとしても高い確率でσ=1以下である」
くらいは言うことが出来るということです。
なので効果量以下は有意差があるとは言えないと設定しておくことで、ある程度「差がないこと」も判断することが可能となります(本来帰無仮説は採択出来ないことを考えると、これは非常に有効な話です)。
効果量とサンプルサイズ
先程の例を見ると効果量1の場合、必要なサンプルサイズは10でした。
1σ程度の差を議論する場合、実はサンプルサイズは10で十分というのは以外な結果に思えます。
そこで気になったので効果量とサンプルサイズの関係を一通りグラフ化してみました。
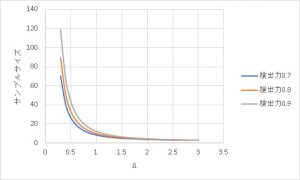
標準偏差の場合はサンプルサイズが30だの50だのとされているのですが、t検定における平均の差の場合は、n=30もあればΔが0.5や0.6まで耐え得るようです。
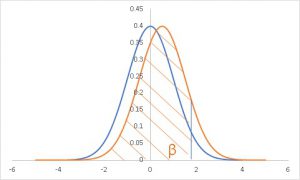
上のグラフは効果量0.5を表現した正規分布です。
オレンジ線が「差が有るのに差がないと誤る確率β」ですので、サンプルサイズ30あればこのような分布でも帰無仮説を事実上採択することが出来るということになります。
まとめ
本を読んで分かった気になっていましたが、実際に効果をグラフ化すると実はよく分かっていなかったと実感出来ました。
サンプルサイズ10程度でもt検定が効果を十分発揮するということはうれしい誤算です。
今後はこのサンプルサイズの設計を行い、更に効果的に検定を行うことが出来そうです。
当サイトを閲覧下さる皆さまは、日々より良い仕事が出来るようになりたいと思われているビジネスパーソンがメインだと思います。 でも「時間が無い」、「セミナー行くの面倒くさい」といった理由で中々学べていない方も多いと思います。 このビジネス動画学習サービスでは、いつでも、どこでもスマホ一つでビジネススキルを隙間時間で学ぶことが出来ます。 youtube紹介はこちら




コメント