工程能力指数(Cpk)は、工程の管理状態を一目で知ることが出来る非常に便利な指数です。
実際にCpkを紹介している書籍やネット情報でも、数字を見ることで管理状態であるかどうかを知ることが出来ると言っています。
しかしながら、Cpkは管理状態を測る以外にも使い道があります。
その使い道を知ることで、管理状態の是正の方針や難易度を予測する事が出来ます。
今回はそんな、Cpkの別の使い道について解説していきます。
動画でも解説しています。
Cpkとは何か？【復習です】
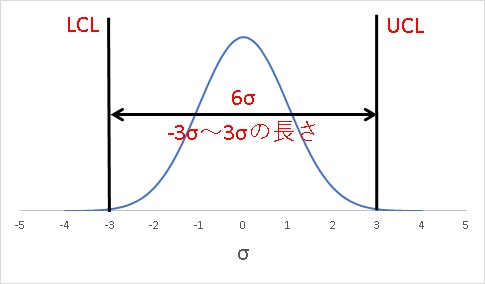
工程能力指数とは、上下限の規格の中に±3σの製品ばらつきの分布がどの程度収まっているかを示した指数です。
詳細は以下の記事を参照してください。
基本的に管理状態の目安としては、Cpk≧1.33です。
これは±4σが上下限規格に収まっていることを意味し、不良の発生率が0.006%であることを示しています。
管理状態以外に読み取るべき情報
ここまでは、Cpkを扱っているサイトや書籍でもよく見られる内容です。
しかし、Cpkの使い道はそれだけではありません。
1.33かどうかを見るだけではダメ
管理状態をCpkで確認出来たとして、その値が想定より小さかった場合(=管理状態にない)、当然改善しなければなりません。
問題はその改善方針です。
製品の”ばらつき”が正規分布をしている場合、修正方針としては
・平均値をシフトさせる
・標準偏差を小さくする
の2つに大別されます。
平均かずれているか、標準偏差が大きいのか
この方針は言われたら当たり前ですが、方針の選択をミスしてしまった場合、労力の割りに効果がいまいちか全く得られないという事になる可能性があります。
基本的に製品の”ばらつき”分布に干渉する場合に覚えておいてほしいことは
・平均値をシフトさせることは簡単
・標準偏差を小さくすることは難しい
ということです。
お風呂のお湯を貯めるというシチュエーションで考えてみましょう。
決められた時間で、決められた量のお湯を入れることを考えた場合、ここでいう不良は決められた量よりも多すぎるか少なすぎるという状態です。
不良：決められた量より多い or 少ない
ここで主な原因が、単位時間当たりのお湯の流量であった場合、蛇口のひねる量を変えるだけでおそらく解決します。
これが平均値がずれている場合です。
対してお湯の出方が脈動している場合、蛇口のひねる量を変えてもおそらく解決しません。原因としては流路の途中に異物が噛みこんでいるのか、そもそも水道局側に何かしらの不備があるのか、考えただけでも調査するところが多そうで、大変そうです。
これが標準偏差が大きい場合です。
製品ばらつきに関しても同様です。
基本的に平均値のズレは、設定値の調節で解決出来る場合が多いですが、標準偏差の是正の場合そもそもの設計から見直さなければ解決しない時も多いです。
設計に関しては、後々変更できない場合も多いので開発段階でよく検討しておくべきです。
それではCpkの是正方針について考えてみます。
平均値がずれているのに標準偏差に対して取り組みをする場合ですが、改善効果が出るまでに時間が掛かりすぎますし、そもそも改善の余地がなく、無駄な時間とお金がかかる可能性があります。
対して標準偏差が大きいのに平均値に対して取り組みをする場合ですが、これはいくらやっても効果が得られることはありません。確実に時間の無駄です。
このように方針を間違えると、徒労となってしまうことになります。
Cpkをうまく使えば、この方針を容易に立てることが出来ます。
Cpが高ければ簡単に改善出来る
定義の中には、Cpkを算出する前に平均の偏りを考慮しないCpを算出するものがあります。
$$Cp=\frac{UCL-LCL}{6σ}$$
これに平均の偏りの補正値として、Kを組み込んだものがCpkです。
逆に言えば、純粋に標準偏差による工程能力指数がCpであると言えます。
この事実は重要です。
Cpkが1.33を割っている場合、次にCpに着目します。
この場合、Cpが1.33を超えている場合は平均値がずれているので、平均値の補正アクションという選択になります。
対してCpの段階で1.33を下回っている場合、現在の製品設計に問題があるため標準偏差の補正アクション(というより設計の見直し)という選択になります。
CpkとCpを見比べることで、工程管理状態の深刻さが浮き彫りになります。
また、日々工程能力指数のデータを取っており一件ずつ比較することが大変な場合は、
$$\frac{Cp}{Cpk}=\frac{1}{1-K}$$
このCpkとCpの比の大きさをプロットをしたグラフを作図することで、改善余地といえるものを見える化することが出来ます。
まとめ
このようにCpkはただ工程の管理状態だけでなく、改善アプローチを示唆する指標としても使用可能です。
このような使用法は、あまりその他資料で言及されているのを見かけませんが、実際に計算したり使ったりすると、ふと思いついたりするものです。
教科書に書いていないからと言って、やってはいけないという事ではありません。
要は何事も、より良くなればいいのです。
皆さんもぜひ様々手法を教科書通りに使うのではなく、色々アレンジしてより良い成果を上げていってください。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ！」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます！！
買い切りタイプなのでお得です。
ぜひお求めくださいな。
コメント