
仕事をするうえで、数値の比較をする機会は非常に多いです。
クレームを出した製品ロットと前後のロット
新開発した洗剤の洗浄力と従来品の洗浄力
地方ごとの製品の売り上げ
店長別で見た売り上げ
等々、枚挙にいとまがありません。
このように数値を比較する際は、算術平均を使用される方が多いと思います。
しかしながら、算術平均はN数が少ない場合は異常値に引っ張られるため、代表値として心もとないです。
また、バラツキを考慮しなければ平均値の差がバラツキの範囲内なのか、有意差なのかが判断できません。
本当は検定を行った方が良いとは思うのですが、検定は1対1に使う手法で複数のデータを一度に確認するうえでは不便です。
それに、バラツキを考慮してグラフで比較したら、それだけで次にどのように分析するべきか結構分かるものなので、まずは小難しい手法を使う前にグラフを書いて確認するべきだと思います。
とりあえず、これからいくつかグラフでの比較を示してみます。
平均だけで比較
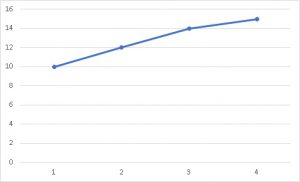
このグラフはある集団の平均値を比較したものとします。
このグラフから見て取れる情報は、右に行くほど数値が大きくなっているということです。
例えば、横軸が時間[h]だったら、時間が経過するほどに大きくなると読み取れるグラフとなります。
バラツキのバーを追加した場合
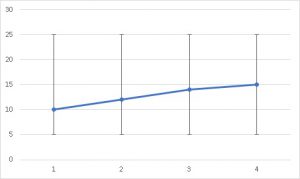
先程のグラフに、最大値、最小値のバーを追加したものです。
これを見る限り、データの推移はすべてバラツキの範囲内に見えます。
先程のように時系列グラフとした場合、時間とともに値が増大しているとは言い難いです。
とは言え、これだけで有意差が本当にないとは言い切れません。
「1」は平均値が10に対して、最大値が25、最小値が5と、分布が極端に最大値に偏っているように見えます。
生データの確認や、ヒストグラム化をするなどして、最大値付近に異常値が無いかを確認すると、もしかしたら、時系列で変化していたと結論付ける可能性も当然あるわけです。
しかしながら、バーを追加したことで、本当に「数値が右に行くほど増加しているのか」を少なくとも疑うことは出来たわけです。
誤った判断を下すリスクを軽減出来たわけです。
つまり何が言いたいの?
数値の比較をするうえで、平均値だけでなく、最大、最小値、もしくは標準偏差等バラツキの要素を追加することで、標本の概要をより正確に知ることが出来ます。
これをするだけで、標本に対する理解度がグッと増します。
また、グラフを作っただけで、ほぼ比較が完了する場合もありますが、今回示した例のように
・バラツキ範囲内でどの数値も有意差がない
・異常値の存在で、分布が歪んでいるだけで実は有意差がある
のいずれか判断出来ない場合も往々にしてあります。
このような状態になったときに、初めて異常値の確認や検定など更に詳細な解析を進めていけばいいと思います。
最初から気合を入れて、すべての解析に検定や、外れ値のチェックなどを入れていては、仕事量が増えると対応しきれません。
なので、自分なりの解析手法の使用ルーチンなどを決めておくと、効率よく解析できると思います。
我々サラリーマンは限られた時間の中で仕事をしているわけですから、簡単に済ませられることは、出来るだけ簡単に済ませるべきです。
統計に限らず、手法や方法論の勉強も大切ですが、道具に溺れて仕事を疎かにしないようにお互い気を付けていきましょう。
出来るだけ手抜きで行きましょう!(良い意味で)




コメント