データを分析する上で、それが質的/量的の別に関わらず統計の手法が必要となってきます。
そして、その統計の手法を説明したサイトや書籍はそれこそごまんとあります。
しかしながら、その統計を解説しているサイトや書籍は手法そのものの説明はしていても、その手法の運用方法について解説したものというのは、ほとんど見かけません。
個人的には、これも統計の利用者数を減らしている要因ではないかと考えています。
統計手法の運用においては、一つのデータ分析において複数の手法を使う事が重要になります。
今回はそんな統計の運用の一助となれるよう、複数の手法の運用について解説していきます。
データは一つの手法だけでは見えてこない!
一つの手法だけで見ようとすると?
一つの手法だけで、分析するとどうなってしまうのか実際に見てみましょう。
例えば、2つの集団を比較するとします。
一番簡単な棒グラフで表現してみると以下のようになります。
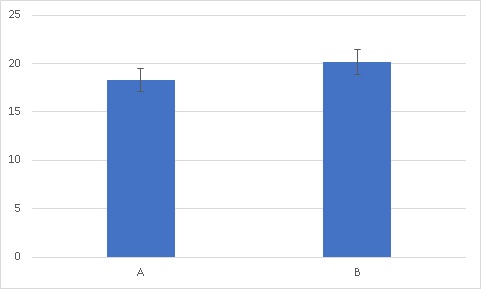
ちなみにこのエラーバーは標準偏差を使っています。
エラーバーに標準偏差を使う際のコツは、以下の記事を参照してください。
このグラフから、エラーバーがギリギリ接触するかしないかの境界なので有意差があるのかないのか、実に微妙なところです。
ここで分析の手を止めてしまうと、有意差については結局モヤモヤした結果となってしまいます。
さて、ここでt検定を実施するとどうでしょう。
結果としてはこうなります。
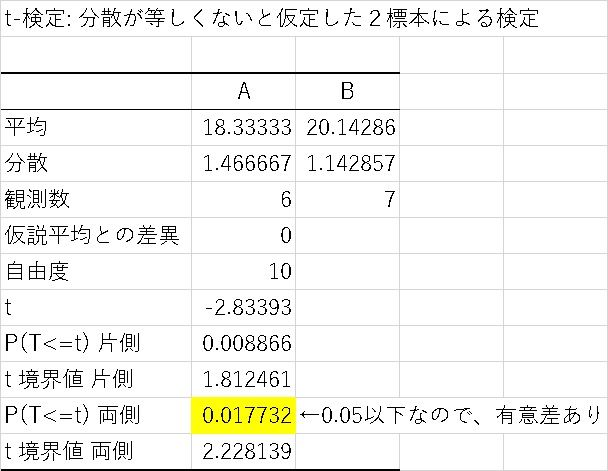
ちなみに、ここではwelchのt検定を使用しています。t検定を使う際には、このweltchのt検定を使うようにしましょう。
理由については、以下の記事をご覧ください。
この結果から、このAとBの平均値には明らかな有意差が存在する事が分かりました。
「だったら最初からt検定だけで十分ではないか」
という声が聞こえてきそうですが、それだと具合が悪いです。
というのも、検定だけでは異常値の有無が判定出来ないのです。
例えば以下のような検定結果があったとします。
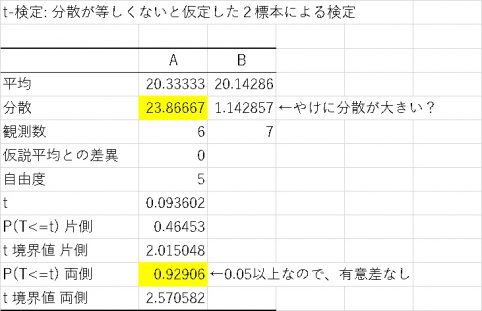
この検定結果からAとBの間に有意差はなさそうです。
実際に平均値の値に差はなさそうです。
ただ、よく見るとAの分散値がやけに大きい。
なんかこの検定結果はおかしい気がします。
しかし、この検定結果だけではここで終わりです。これ以上この結果だけでは分析を進める事が出来ません。
ここで逆に棒グラフ(平均±標準偏差)で見てみましょう。
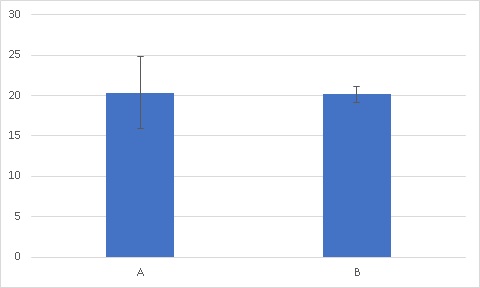
このグラフを見ると、Aの”ばらつき”はやはり大きいようです。ですがやはりここでも先ほどの検定以上の情報は得られそうにありません。
しかし、ここで諦める私ではありません。
もう一つ見てみます。
次は平均値に範囲のエラーバーをつけてみます。
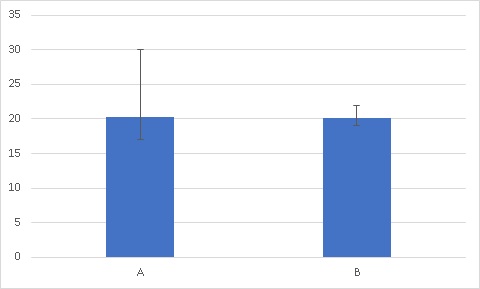
上方のバーは最大値、下方のバーは最小値です。
標準偏差は一つだけの値なので、平均値から均等にしか伸びません。
対して、最大値~最小値の範囲をエラーバーに適用すると、分布の偏りを簡易的に可視化することが出来ます。
さて、このグラフに注目するとAはやたら上方にバーが偏っていることが分かります。
これは一つ異常値が混ざっているために分布に偏りが生じた結果起きたものです。
つまり、先ほどの有意差なしという検定結果は、異常値の影響を大きく受けている可能性が高く、正しく判定出来ているのか疑わしいという結論に至るわけです。
さてここでオチなのですが、実はこのAとBの比較は、最初の例で有意差ありと判定されたAとBの一つを異常値と入れ替えただけのものなんです。
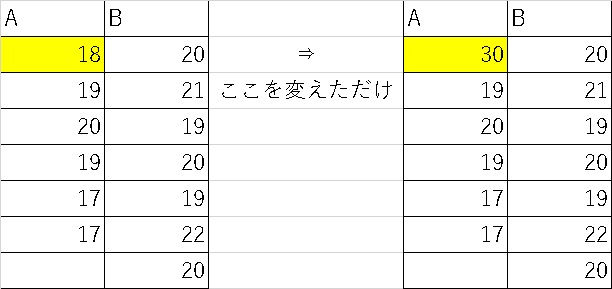
たったこれだけの変化ですが、検定結果だけに注目していると、とても気づくことは出来ません。
このようにデータ分析は一つの手法に頼っていると、思わぬ落とし穴に落ちやすいのです。
一つの手法で見えるのは一面だけ
データというものは、様々な一面を持っています。
そして統計的分析手法というのは、その内の一面のみを示すものです。
物事は一つの面だけ見たのでは、正確に把握しきれないものです。
例えるなら、富嶽三十六景。
富士一つとっても、見る景色によって様々な情景を見せるのです。

人も情景も、そしてデータも一面的には語れないものがあるという事です。
複数の手法で多角的に捉えよう
基本的には、データを分析しながら
「この手法でみたらどう見えるだろう?」
と試行錯誤しながら分析していくのが望ましい為、こういう手順で見たら完璧というものはありません。
これが中々解説する書籍が少ない所以だと思います。
とは言っても、正直取っ掛かりぐらい欲しいものです。
という事で、私が普段分析する際に多用するルーチンを紹介いたします。
グラフ&検定を併用しよう
先に紹介したように、まずはグラフを書きましょう!
単純比較なら棒グラフ
時系列とう何かしらの変化に伴う場合は線グラフ
2つの変数の関係性なら相関図
などなど
まずはグラフを書くことで、そのデータに対してのイメージが湧いてきます。
そしてそのグラフの印象を裏付ける意味で検定を実施しましょう。
グラフで見える差というものが、検定(=”ばらつき”を考慮した上での比較)において有意か否かを明確にする。
このようなルーチンを回すだけで、分析効率はかなり上がるはずです。
層別/総合二つの観点で確認しよう
層別はQC7つ道具でもカウントされる、基本であり重要な手法の一つです。
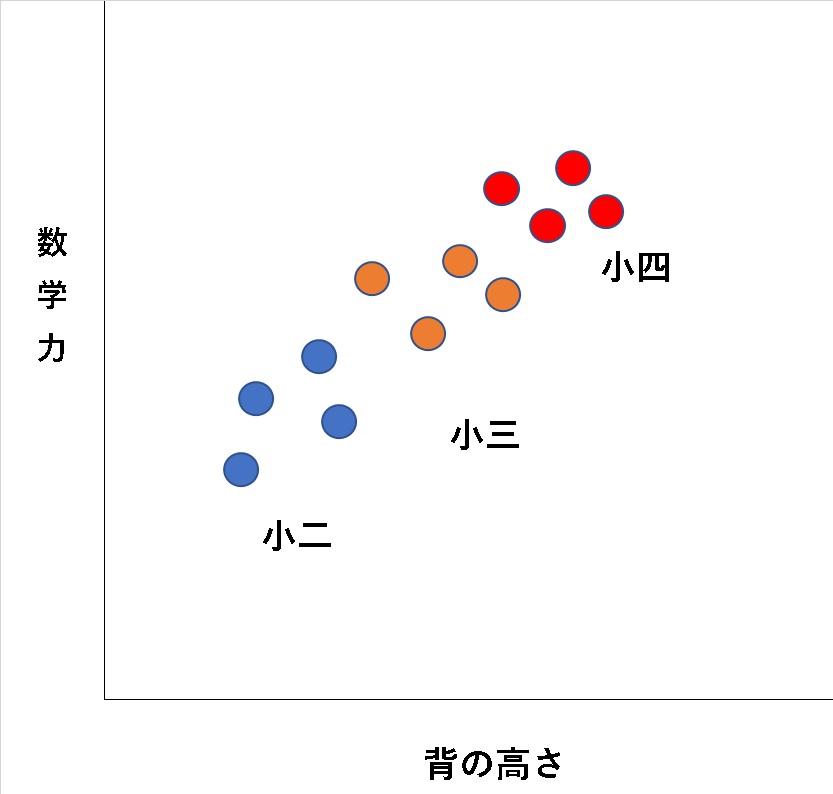
例えばこのグラフの場合、一見すると背の高さと学力に相関があるように見えます。
しかし、学年という要素で層別すると、実は学年が高い為に学力が上がっているのであり、背の高さは本質的に因果関係とは関係が無いという事が分かります。
ただしこの層別というものは、どこまで細かくすればいいのか分からなくなることが多いです。
時間別/人別/場所別/材料別/設備別/・・・思い浮かぶ層は枚挙にいとまがありません。
このような場合、思いつくままに層別してみてグラフがどのように変化してみるのか一つ一つ観察するのが有効です。
また、層別だけでなく、完全に層を丸めて総合的に見てみるのも手です。
物事を観察するときのポイントは、鳥の目と虫の目です。
層別だけでなく、総合的に見るのも重要な視点なのです。
まとめ
今回は、統計的にデータを分析する際に必要な、多角的に分析するという事を紹介しました。
グラフ/検定や層別/総合という見方を、分析の取っ掛かりにするだけで分析能力は格段に向上するはずです。
しかし覚えておいて欲しいのが、最も重要なのは手法と手法を行き来する際に、思考をはさんで欲しいという事です。
グラフ化して観察して、
「”ばらつき”は同じくらいだし、平均値には差がありそうだから、t検定を使ってみよう」
⇒t検定を実施
相関図化して観察して
「なんか背の高さと学力が相関有りそう。なんでだ?とりあえず層別で色々分解してみよう」
⇒層別分析
このように、一つの手法を終えた後に思考、考察を入れないと次に選択する手法がおかしなことになってしまいます。
分析⇒思考⇒分析
このサイクルをルーチンに乗せて回していければ、アクションにつながる分析が実施出来ると思います。
参考にして頂けると幸いです。




コメント