統計学ぶ上で、第一の関門が検定、推定であるとすれば、第二の関門は多変量解析だと思います。
個人的には多変量解析は、検定や推定に比べても難しいと思います。
解析方法において、行列や微分がふんだんに含まれますからね。
ですが、一度理解出来るとこれまで分析出来る対象とすら思っていなかったようなものも分析出来るようになります。
今回は多変量解析のうちの一つ、主成分分析を紹介します。
主成分分析は行列の知識が無くとも、エクセルの機能で解を得ることが出来る分析手法です。
まずは行列を抜きにして、実際に使える主成分分析を学んでいきましょう。
今回はこちらの書籍を元に解説していきますので、詳細をもっと知りたい方は、ぜひ一度読んでみて下さい。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
主成分分析を理解しよう

主成分分析って何?
主成分分析とは、多変量解析の一種です。
重回帰分析を勉強し終わった次の段階で、勉強し始める事が多い手法のように思います。
(アナタもそうじゃないですか?)
主成分分析を一言で言うと、
「沢山のyを一つのyに合成する手法」
って感じでしょうか。
一見すると、何の役に立つのか分かりづらくないですか?
指標の数を絞って何の役に立つのって。
ですが、実は我々は普段から似たような事を、知らず知らずのうちにやっていたりするんですよ。
例えば学力だと、理科、数学が得意で歴史、国語、英語が苦手だと、理系が得意で文系が苦手と表現しますよね?
FMEA(故障モード影響解析)でも、影響度、発生度、検出度という3つの指標を算出した後に、その3要素の掛け算であるRPNという総合指標を算出します。
このように我々は、日頃から複数の指標を一つに合成するという行為を、実行しているわけです。
なぜか?
それは判断基準は、少ない方が判断しやすいからです。
指標が沢山あると情報量が多いので、いいじゃんと思ってしまいますが、ごちゃごちゃしているとどれを採用して判断していいのか分からんのです。
国語と英語と歴史の点数のどれか一つで判断したら、適切な判断とは言えません。
かといって、この3つを単に足し算しても、なんか合成指標として正しいのか疑問が残ります。
故に、複数の指標を適切に合成する手法、主成分分析に需要が生じるという訳です。
主成分分析はバラツキが大きくなるように合成する
それでは主成分分析は、いかにして指標を合成するのか考えてみましょう。
先程でもふれたように、学校の成績を軸に考えてみましょう。
国語、英語、数学で個々人の学力を把握する際、通常学校では合計点で生徒間の学力を比較します。
主成分分析はこんなダセェ方法は取りません。
主成分分析では一つ一つの生徒の成績が最もばらつきが大きくなるように、各成績の和を作ります。
例えば、以下の図をご覧ください。

元変量と書いた図は、5つの●の区別がつきずらいです。
では元変量のから少し見る角度を斜めにして、下の新変量という角度で見えるようになったらどうでしょう。
5つの●の区別がつけやすくないですか?
見る角度を変えるだけで、差がつけやすくなるというのは、良くイメージしやすい話ですが、これを何を目印にして、見る角度を決定すれば良いのでしょうか。
その目印とはズバリ、ばらつきです。
5つの●が区別がつくというのは、●同士の距離が離れているからです。
つまり、●同士の位置が大きくバラついているため、区別がつくのです。
故にばらつきの指標(ここでは計算のしやすさから分散を使います)を、目印にすれば最も合理的に指標を合成出来るという訳です。
これが主成分分析の基本原理になります。
主成分分析の実施方法

合成変量の作り方
それでは、とりあえず主成分分析の合成した変量を実際に作ってみましょう。
やってみりゃイメージもつくってもんです。
3変量x,y,zで考えてみましょう。
各変量に重みの定数a,b,cを掛けて以下のような合成変量pを考えます。
$$p=ax+by+cz$$
もろ重回帰式ですね。
ただ、このままだと色んなa,b,cが設定されて一つのpが求められないので、一個条件を設定します。
$$a^2+b^2+c^2=1$$
この条件下で合成変量を考えるのです。
このpの分散
$$s_p^2=\frac{1}{n}\sum_{i=1}^{n}{(p_i-\overline{p})^2}$$
が最大になるa,b,cを決めれば良いのです。
「ソルバー」による主成分分析の方法
ですが、この分散の最大値を求める過程が中々に至難です。
行列とか出てきます。うっとうしいです。
そこで今回はそのあたりを、エクセルアドインのソルバーに頼って答えを得る方法を解説します。
力技です。
例として学校の成績で考えてみましょう。
各個人の数学x、理科y、社会u、英語v、国語wの成績の主成分分析を行います。
$$p=ax+by+cu+dv+ew$$
$$ただしa^2+b^2+c^2+d^2+e^2=1$$
におけるpの分散の最大化を考えます。
pは主成分、a,b,c・・・は主成分負荷量と呼称します。
エクセルで以下のような表を作ってみてください。
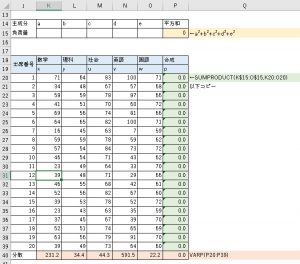
・各出席番号ごとに各教科の成績を並べる。
・成績の表の上に、主成分負荷量を入力するセルとその平方和の計算式を入力した式を並べる
・合成の行にsumproduct関数で
$$=ax+by+cu+dv+ew$$
となるように式を入力する。
・各成績、合成変量pの分散varp関数を入力
これで準備は整いました。
次にアドイン「ソルバー」を開きます。ソルバーが入っていない場合は読み込んでください。
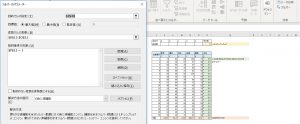
【目的のセル】には合成変量pの分散を算出セルを指定します。
【目標値】は最大値を指定します。
【変更セルの変更】には、a,b,c,d,eを指定します。
制約条件の対称には、a,b,c,d,eの平方和のセルを指定します。
後はこれを実行したら、合成変量pの分散が最大となるa,b,c,d,eが算出されます。
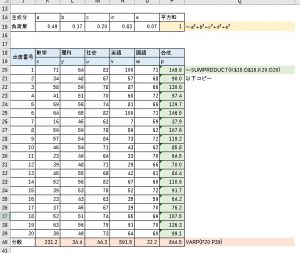
このソルバーでは、主成分pの分散が最大になるように主成分負荷量を制約条件の元、色々動かして値を導きます。
これなら、簡単に主成分分析を実行することが出来ます。
しかしながら、この導いた主成分が全然データの情報(分散)を取り入れていないのであれば意味がありません。
誤った解釈をしてしまう可能性があります。
故に導き出した主成分が、どれだけデータの個性を取り入れているのかを調査する必要があります。
更に今ここで出した主成分がすべてのデータの個性を表現出来ていない場合、残りのデータの個性も何とか表現したいというのは、人情ってもんです。
という事で、次に主成分の寄与率と第二主成分の導き方について解説します。
主成分の寄与率と第二の主成分

主成分の寄与率
先程述べたように、主成分分析は分散の大きさ材料に指標を合成します。
故に主成分が合成前のデータをどれだけ取り入れられたのかは、
「全データの分散に対して、主成分の分散はどれだけか」
という指標で定量化出来ます。
この主成分の分散の度合い(情報量の度合い)を寄与率と言います。
以下の表の場合寄与率Cは

$$C=\frac{s_p^2}{s_x^2+s_y^2+s_u^2+s_v^2+s_w^2}$$
になります。
この場合、分母は各変量ごとに分散を導いてそれを総和してください。
実際に計算すると以下のようになります。
$$C_1=\frac{845.5}{231.2+34.4+44.3+591.5+22.2}=0.91$$
この場合、主成分pは全データの分散の91%を表現していると言えます。
かなり当てになるので、この主成分で生徒の総合学力を判定することは正しいようです。
ただ、残り9%はどこかに行っちゃったようです。
コイツも何とか拾い上げたいなと思う訳ですが、そういう時には第二主成分を算出する事になります。
第二主成分
もういんじゃね?9%とかって感じはありますが、毎回90%以上の保証ってないんですよ。
主成分が70%や60%程度しか説明出来ない場合って普通にありますからね?
ってなったら残りの30%や40%の情報を知りたいわけじゃないですか。
という事で、残りの情報を表す第二主成分の導き方を説明します(対して最初に導いた主成分は第一主成分と言います)。
まずは、各生徒、各教科(変量)のデータの「残りかす」を算出します。
残りかすとは言葉が悪いですが、これは第一主成分では説明がつかない数値を抽出するということです。
例えば数学xの場合式で表すと
$$x’=x-ap$$
になります。出席番号1の数学xの場合
$$71-0.49×149.9=-2.7$$
となります。主成分149.9点のうち49%が数学xの得点寄与分ですので、それを引いてあげるのです。
そんな感じで各生徒、各教科で計算した表がこちらになります。
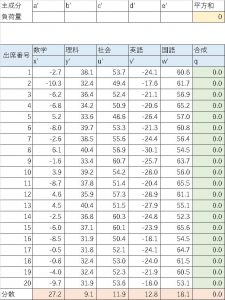
この表に対して、第一主成分の時と同様にソルバーで負荷量a,b,c,d,eを導くと
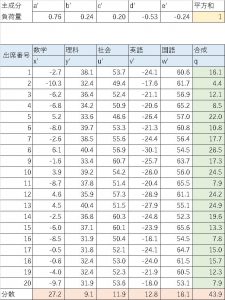
となります。こうして導かれたqが第二主成分になります。
この値は数学の時に大きなプラス(0.76)、国語の時に大きなマイナス(-0.53)の負荷量を示しているので、理系、文系能力の好悪とでもいえるものを表しているようです。
この値qを通常のx,y・・・で導くには
$$q=0.76x’+0.24y’+0.20u’-0.53v’-0.24w’$$
に
$$x’=x-0.49p$$
といった先ほどの””残りかす””の算出式を代入すると
$$q=0.76(x-0.49p)+0.24(y-0.17p)+0.20(u-0.20p)-0.53(v-0.83p)-0.24(w-0.07p)$$
$$q=0.76x+0.24y+0.20u-0.53v-0.24w$$
このようにpがうまく消えてくれます。ですので実使用の場合はソルバーで算出したa’、b’をそのまま使って大丈夫です。
さてこの第二主成分の寄与率ですが、
$$C_2=\frac{43.9}{231.2+34.4+44.3+591.5+22.2}=0.05$$
となります。残り9%のうち5%が第二主成分で説明できることが分かりました。
これを繰り返すと第三、第四主成分も導くことが出来るようになります。
解釈はアナタ次第
これでエクセルで主成分分析が出来るようになりました。
今の処理で、5次元(国数英理社)のデータが2次元まで合成出来たのですから、判断が非常にしやすくなったはずです。
ただ、ここで気を付けるべきなのは、主成分の軸の解釈は分析者自身で行わなければならない、という事です。
先程第1主成分は総合得点、第二主成分は理系、文系の好悪と表現しましたが、これは飽くまで合成した指標の数字の大きさと、合成前の数字の関係性から推察した内容に過ぎません。
主成分分析は、その合成した軸がどういった意味をもたらすのかは教えてくれないのです。
この辺りは分析者の腕に見せどころです。
これまで培ってきた知識を動員して、推察してみて下さい。
ただ一つヒントとして、第一主成分は基本的には総合力を表現すると言われています。
また、第一主成分、第二主成分を散布図としてデータを可視化するという分析も良く行われます。
可視化したグラフの分布状態から、特に第二主成分が何であるのか判断すると、比較的容易になるかもしれません。
まとめ
主成分分析は、我々が普段行う指標の合成を合理的に行う手法です。
今回紹介したようにエクセルでも実行できますし、EZR等の統計ツールを使えば、より簡単に分析可能です。
主成分分析が使えるようになれば、これまで解明できなかった傾向も分析出来るかもしれません。
ぜひ、試してみて下さい。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ!」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます!!
買い切りタイプなのでお得です。
ぜひお求めくださいな。





コメント