マハラノビス距離という単語を聞いたことありますか?
マハラジャっぽい響きだなぁと思われたとも思いますが、それもそのはずでインドの統計学者マハラノビスさんが作った手法です。
元々は考古学において骨の発掘調査をする際に、既知の骨のデータからの距離を定義して骨の種類を定量的に判別出来るようになったそうです。
集団の似てる似てないを、距離という分かりやすい指標で表現出来るので多変量解析におけるクラスター分析、品質工学におけるMT法など様々な手法に活用されています。
つまり、統計学における高度な手法を覚えるにあたり、このマハラノビス距離への理解は必須という訳です。
今回はそんな多変量解析を理解する上で重要なマハラノビス距離を分かりやすく解説します。
マハラノビス距離のイメージ

グラフのイメージ
マハラノビス距離を理解するには、以下のような2変量の散布図を使うのが良いです。
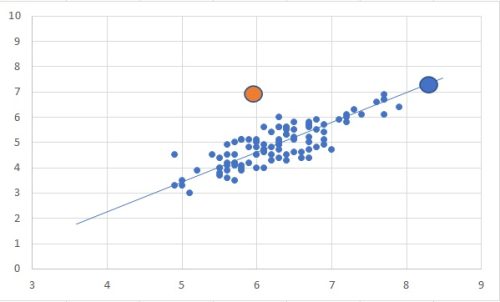
相関性があるデータに対して、青丸と橙丸があるとします。上記なかんじで。
これを見てどちらが外れた値に見えますか?
おそらくほとんどの方が橙丸の方を選ぶと思います。
こんな書き方すると変に勘繰られるかもしれませんが、ご安心ください。橙丸が外れ値で合っています。
問題はこの橙丸を数学的に判別するのが意外と難しいという点です。
通常思いつくのはデータ群の平均値との距離という考え方です。
ただ、この平均値との距離では橙丸のほうが青丸より近く正しい判別が出来ません。
一つ工夫が必要です。
その一工夫はばらつきの情報です。
こんな風にばらつきの情報を楕円の半径として表現してみましょう。
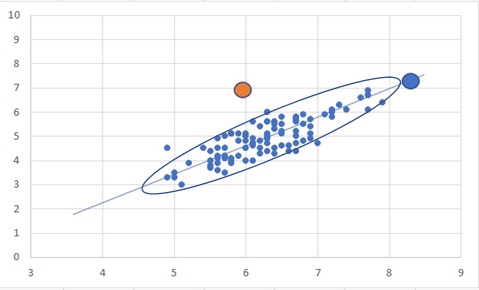
中心を平均値として半径を1とした場合、青丸と中心の距離は半径1とほぼ等しいと言えるでしょう。
対して、橙丸と平均値の距離は楕円の円周部からかなり離れていますので、半径2くらいの距離は離れていると言えます。
このようにデータの分布は不均等の場合が多いです。そんな歪みを持ったデータに対して単に平均値との距離を活用していたのでは対応しきれません。
その分布の歪み、データの向き毎に異なるばらつきの大きさの違いを使う事で適切にデータ群と個々のデータの違いを正確に把握することが出来ます。
マハラノビス距離はこの概念を多次元に拡張したものになります。
統計的なイメージ
次に数式で表現してみます。
マハラノビス距離の最も簡単な式は一次元における式です。
以下になります。
$$D=\frac{|x-\bar{x}|}{σ}$$
データと平均値の距離が何σ分あるのかを表しています。
標準偏差σと同じ距離離れていればD=1
標準偏差σの2倍離れていればD=2になります。
このマハラノビス距離Dが大きくなるほど、元々の集団から離れていること、つまり似ていないという事を示すわけです。
これを集団同士の比較に応用すれば、一見しては分かりづらい数字の羅列である集団の似ている似ていないを判別出来るわけです。
ただし先ほどの式では1変量(=1次元)にしか対応出来ません。最初のグラフである2変量にすら対応出来ないのです。
これを多変量(=多次元)に対応させるための一般化した式が必要になります。
マハラノビス距離の算出
データの分析
先ほどの式を多変量に一般化した式が以下になります。
$$D=\sqrt{(YR^{-1}Y^T)}$$
ただし
Y:標準化したデータのベクトル
R-1:相関行列の逆行列
を指しています。こちらの文献をもとに算出していますので他の書籍と若干描写が異なるかもしれませんがやっていることは一緒です。
ちなみにTは転置行列であることを指します。
Yというデータのベクトルがデータと平均値の差を表現しており、R-1がσを表現しています。
これ行列を活用するって話なんです。久々に行列に触れた方もいらっしゃると思いますのでとりあえず実例を示しながら解説していきます。
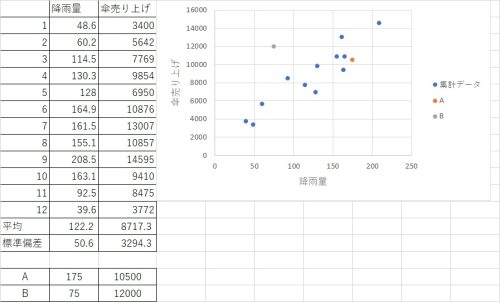
降雨量と傘の売り上げというデータ群があります。その中でAとBというデータがデータ群に対して近いか遠いかをマハラノビス距離で表してみましょう(答えは見た目的にBなのは分かり切っているのですが)。
まずはデータ群を標準化します。標準化とは正規分布を標準正規分布にする処理と同じで
$$z=\frac{x-μ}{σ}$$
です。ちなみにこのデータ群を母集団としてとらえるので母標準偏差として算出します。エクセル関数だとSTDEV.Pで出してください。
そしてAとBの標準化ですが、この元となるデータ群の平均値と標準偏差を用いて行ってください。この場合降雨量なら平均122.2、標準偏差50.6を用いて
$$A=\frac{175-122.2}{50.6}=1.043$$
になります。
このようにして標準化すると以下のようになります。
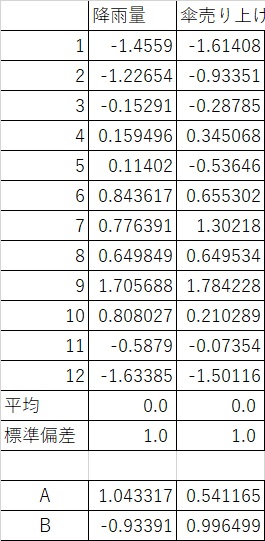
これでまずYが出ました。AのYは1.043、0.541でBのYは-0.934、0.9965です。
行列として表現すると
$$Y_A=\begin{pmatrix}
1.043 & 0.541
\end{pmatrix} $$
になります。またYの転置行列YTは
$$Y_A^T=\begin{pmatrix}
1.043 \\
0.541
\end{pmatrix}$$
になります。=TRANSEPOSE(配列)で転置行列を作ることが出来ます。
必要なセル数を選んで(今回の場合2×2マス)、1マスに==TRANSEPOSE(データの行列)を入力し、[ctrl]+[alt]+[enter]を同時に押すとすべてのマスに逆行列が入力されます。

残りはR-1ですたい。
まずは相関行列を出します。相関行列とは相関係数の行列です(まんまやん)。
相関行列はエクセルの分析ツールで計算可能です。
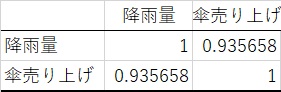
上記のように降雨量と降雨量の相関係数は1になります。
降雨量と傘売り上げの相関係数は0.94です。こんな感じで各データの交点に相関係数を並べた行列が相関行列になります。行列として表記すると
$$R=\begin{pmatrix}
1 & 0.94 \\
0.94 & 1
\end{pmatrix}$$
になります。次にこのRの逆行列を算出します。
エクセルでは=MINVERSE(配列)で計算出来ます。
必要なセル数を選んで(今回の場合2×2マス)、1マスに=MINVERSE(相関行列の配列)を入力し、[ctrl]+[alt]+[enter]を同時に押すとすべてのマスに逆行列が入力されます。

$$R^{-1}=\begin{pmatrix}
8.03 & -7.51 \\
-7.51 & 8.03
\end{pmatrix}$$
大体こんな行列になったと思います。これで材料がそろいました。
最後にこれらをすべて掛けます。
$$D_A=\sqrt{Y_AR^{-1}Y_A^T}=\sqrt{\begin{pmatrix}
1.043 & 0.541
\end{pmatrix}\begin{pmatrix}
1 & 0.94 \\
0.94 & 1
\end{pmatrix}\begin{pmatrix}
1.043 \\
0.541
\end{pmatrix}}$$
行列の積は=MMULT(配列1,配列2)で出来ます。今回の場合は
=(MMULT(MMULT(Yの配列、R-1の配列),YTの配列))^0.5
という関数で入力すれば計算出来ます。
DA=1.61
DB=5.38
という数値になりましたでしょうか。
ここから見るに、AよりBのほうが3~4倍集団から離れていることになります。グラフの見た目とも合致しそうな数値になっているんじゃないでしょうか。
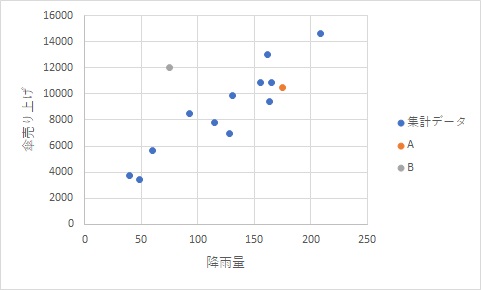
マハラノビス距離の問題点
マハラノビス距離を使えばデータの乖離具合というものを測ることが出来ます。
しかしながらいつでも使えるという訳ではありません。うまく計算出来ないシチュエーションというものがあります。
それが変数同士に多重共線性がある場合です。
多重共線性とは簡単に言うと情報のダブりです。
相関行列において、変数1と変数2の相関係数が0.99くらいに近いと逆行列がきちんと算出されないのです。
逆行列が計算されないということは、それを使ったマハラノビス距離もちゃんと計算されないという事です。
変数が少ない場合は目視で確認も出来ますが、変数が100以上とかいっぱいあるとそれも現実味がありません。そんなときはヒートマップを使いましょう。
エクセルの相関行列上で条件付き書式を適用すれば数値が高いところを赤くすることが出来ます。それで見つけやすくするのです。
また、マハラノビス距離があてになるかどうかを確認する術ですが、実はマハラノビス距離に活用した元のデータ群の各マハラノビス距離に対して
$$D^2 / n$$
した数値の平均値が1になるという性質があります。
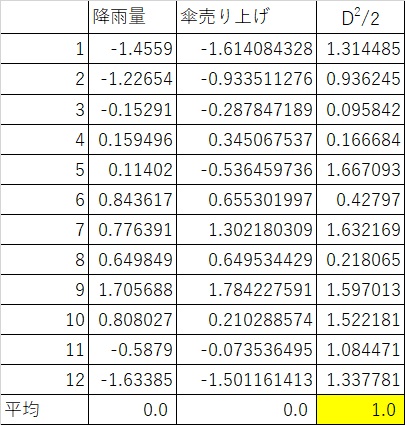
今回のデータでは変数が2つあるのでマハラノビスの2乗を2で割っています。
変数が3つの場合はD2/3です。
その値の平均値はかならず1になるのです。
この平均値が1から小数点レベルでもずれている場合は、多重共線性で阻害されている可能性があります。十分チェックしましょう。
まとめ
多変量のデータを扱う時に、各データが似ているか否かは非常に重要になります。
その情報に立脚した手法としてクラスター分析やMT法などがあります。
そんな各データの距離を汎用的に測定する手法としてマハラノビス距離があるのです。
ばらつきによる歪みを活用することで、データ間の距離を正確に測る事が出来ます。
この手法を知っていれば、多変量解析を理解するのにも助かりますし、単体として活用することも可能です。正常品とクレーム品の差を多変量的に見ることが出来るわけですからね。
今回示したようにエクセルでも計算可能ですので、ぜひチャレンジしてみてください。
手を動かすことで理解力が高まると思います。
また、計算のイメージがわきにくい方はこちらもどうぞ。
動画で解説しているので、より具体的に計算過程が分かると思います。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント