統計学において、検定というスキルは非常に使用頻度の高いものです。
なんといっても、
「この2つの値って差があるって言えるのかな?言えないのかな?」
と言った悩みをある一定の確率の元、断定してくれるのですから。
そんな便利な検定ですが、実はこんな勘違いをされやすい手法でもあります。
それは、
『有意差なしを積極的には言及出来ない』
という点です。
つまり有意差ありと出た場合は、
「よしっ!有意差あるぞ!」
と言えるのですが、有意差なしとなった場合
「有意差がないかもしんない」
くらいにしか言えないのです。
でもでも、2つの数字を比較するとき、必ずしも差が有ることを言いたいだけって事、ないですよね?
差が無い事も積極的に言いたい場合もありますよね?
という事で今回は、検出力を利用した等しい事を採択する検定の方法を紹介いたします。
動画でも解説しています。
参考文献としては、以下を使用していますので、もし詳細を知りたい方は、ぜひ読んでみて下さい。
検出力に言及した本で日本で一番有名な書籍です。
検定で積極的に有意差なしを採択出来ない理由

分布の距離によって検定結果の意味合いが異なる
詳細は以下の記事を参照頂きたいのですが、
ポイントは分布の距離です。
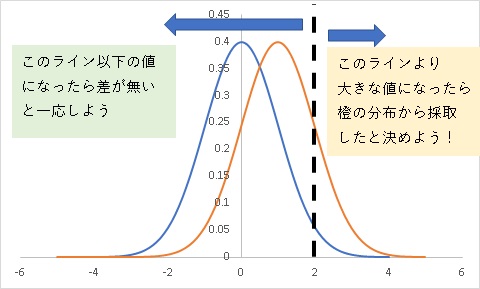
元の分布と比較対象の分布に平均値の差があまりない場合、分布の大部分が重なります。
有意差がないという結果は、その大部分から採取されたサンプルなのですから、元の分布だけでなく比較対象の分布からも採取される確率は非常に大きいのです。
それ故に検定において、有意差が無いという判断は軽はずみにすることが出来ないのです。
それでは、どうすれば良いのでしょうか?
効果量を設定しよう
先程は有意差が無い事に着目していましたが、実は有意差ありも手放しで受け入れるというのは、結構危険です。
分布間の距離、つまり平均値が近い分布同士で検定を行うと、有意水準5%でも結構比較対象の分布が被ってくるからです。
結局のところ、有意差が有ろうが無かろうが分布間の距離が一定以上離れていないと、判断を間違える可能性があるという事です。
この分布間の距離を考慮して検定を行うためのポイントとして、以下の3つのキーワードが存在します。
効果量、検出力、サンプルサイズ
です。
効果量は以下の式で表されます。
$$Δ=\frac{μ-μ_0}{σ}$$
これは分布の距離、つまり平均値の差が標準偏差の大きさに対してどの程度離れているのかを示しています。
ちなみに、分子の平均値の差は解析者が決めます。
「このくらいの平均値の差があったら、うまく検出してほしい」
という差を見込んで設定する事になるのです。
このあたりの決め方としては、これまでの観測例とかからの技術的な理由で設定するのがセオリーです。
次に検出力ですが、これは1-β、つまり1-第二の過誤の確率であり、有意差が存在する確率を指します。
この1-βは80%が望ましく、この値は効果量とサンプルサイズに密接に関係します。
つまり、検出力を80%とし、効果量をこれまでの技術的見地から設定すると、適切なサンプルサイズが導けるという訳です。
この辺りの解説は過去別の記事でも紹介していますので、もっと詳しく知りたいゾって方はそちらを参照ください。
『有意差がない』を積極的に採択する方法

検出力80%のサンプルサイズで検定をする
見出しにネタバレを書いてしまいましたが、検出力80%となるようなサンプルサイズで検定を行えばよいのです。
先述したように、サンプルサイズは検出力と効果量が決まると算出出来ます。
検出力は80%が理想(高すぎるとサンプルサイズが多すぎて、有意差がないものも有意差ありとなる)なので固定します。
効果量は平均値の差を過去の知見から決定し、標準偏差はとりあえずサンプリングからの不偏標準偏差を使うと良いです。
そこまで決まると、自動的にサンプルサイズを算出出来ますので、そのサンプルサイズで検定を実施します。
有意差ありの場合は、再度検出力を計算すると80%を超えるはずです。
有意差なしの場合は、少なくとも効果量で設定した平均値の差以上には差が無いと判断出来ます。
この方法を使えば、有意差なしを積極的に採択出来ます。
効果量からのサンプルサイズの決定方法はEZRだと、数字を入力するだけで自動的に算出されます。
ぜひ、こちらの記事を参照してみて下さい。
サンプルが多すぎる場合はエクセルのサンプリングを活用しよう
検出力を左右するのはサンプルサイズです。
事前検証(あらかじめ効果量とサンプルサイズで検出力を算出する、検定の設計)で適切なサンプルサイズが導かれます。
手持ちのサンプルサイズが小さい場合は、もっと増やしてくれなんしって感じですが、実はサンプルサイズが多すぎる場合も良くありません。
基本的に統計においては、サンプルサイズは多いに越したことはないとされる事が多いですが、検定の場合は違います。
サンプルサイズが多すぎると、検出力が上がりすぎて、第一種の過誤を引き起こす可能性があるのです。
故にサンプルサイズが多すぎる場合は、そこから検定に使うデータをランダムに引き抜いてやる必要があります。
ですが、この引き抜き作業が結構だるいんです。
人間が手作業でランダムに作業をするのは、かなり困難です。
どうしても恣意的な選び方になってしまいます。
そのような時は、エクセルのサンプリング機能を使いましょう。
分析ツールを選ぶと、サンプリングという機能があります。
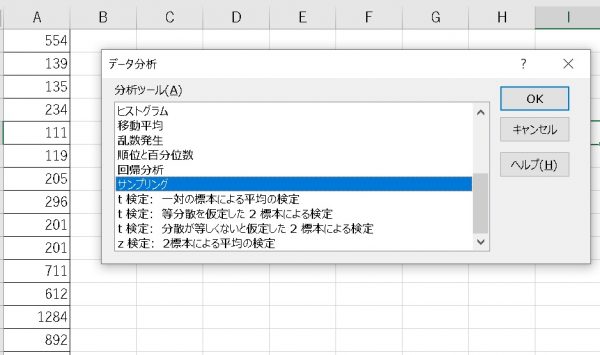
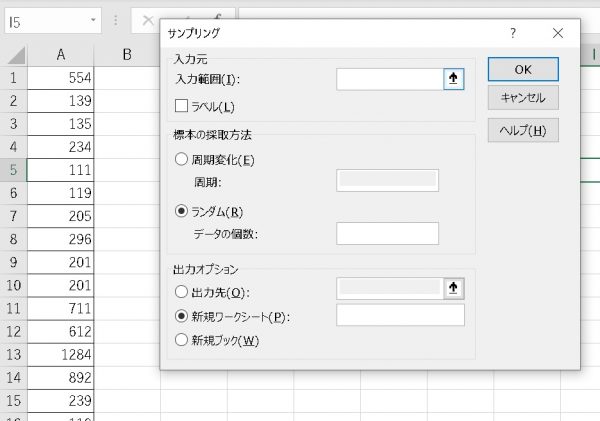
これを選ぶと次に、サンプリングするデータ群を【入力範囲】に選択します。
次に、【ランダム】にチェックをつけた状態で、【データの個数】を入力します。
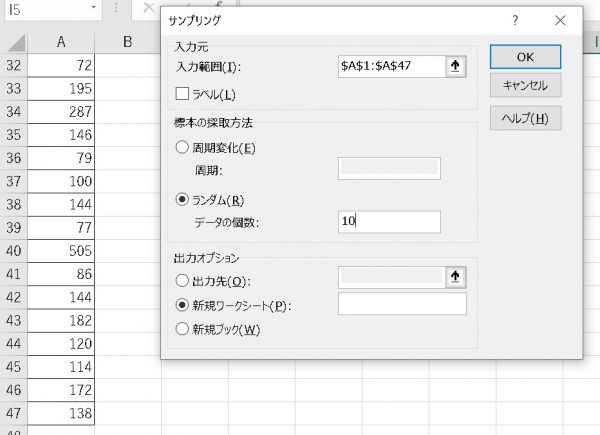
後は出力先(出力オプション)を選んでOKすると、ランダムに指定した数のサンプルをサンプリングしてくれます。
こうする事で、サンプリングが多すぎた場合でも適切なサンプルサイズで検定を実施出来るという訳です。
結構便利ですので、ぜひ使ってみて下さい。
まとめ
検定を行う時は、サンプルサイズが肝です。
ここをうまく設計できないと、有意差がない場合の判断もあやふやになりますし、有意差がある場合もどれだけ確かなのか断定出来ません。
EZRを使えば、サンプルサイズは簡単に設計出来ますし、エクセルのサンプリング機能を使えば適切なサンプルサイズに変換出来ます。
ぜひこれらを使いこなして、一段レベルの高い検定を行っていきましょう。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント
Great content! Super high-quality! Keep it up! 🙂