研究開発に限らず、品質保証、製造現場、生産技術などなど様々な部署において、問題を解決したり、課題を達成する上で実験という活動は避けて通れません。
通常実験というものは、仮説があってそれを立証するために様々な条件を組んで実施されます。
故に実験の成否は、実験の組み方にあると言っても過言ではありません。
今回は実験の回数を効果的かつ最小限にする直交表の概念を紹介します。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
直交表って何?
実験の組み合わせは膨大
実験をする際、要求する性能の項目が出来るだけ最大化する数々の要因を様々な水準に振って検証します。
例えば、植物の生育具合を最大化する目的を達成するために、水、土、光という3つの要因が挙げられるとします。
更に各要因の水準を上げるとすると
水:硬水/軟水
土:粘土/腐葉土
光:光有り/光なし
というように上げることが出来ます。こうなるとすべての組み合わせを見るためには、実験回数は
$$実験回数=2^3=8回$$
となります。
まだ何とかなりそうな実験回数に見えますが、ここにもう一つ肥料という項目2水準を加えると
$$実験回数=2^4=16回$$
になります。このように基本的に実験の組み合わせの数は
$$実験回数=水準数^{要因数}$$
と要因が増える事で指数関数的に組み合わせの数が増加していきます。
そして、実際に実験する上で一つ二つの要因検証で足りるわけが無いというのが現実です。
そして、よく行われるのが、本命の1~2要因に対して水準数だけやたら増やして適切な水準が無いかどうかを繰り返す実験だと思います。
ですが、実際にその本命の要因が実は大して効果に寄与しないものであった場合、当然時間が無駄になるわけです。
故に水準を振る前にまずは、重要な要因を見つける事が必要なわけです。
そして効果的に要因を見定める手法が分散分析法であり、最小限の実験の組み合わせを提言するものが直交表になります。
直交表で実験回数を減らそう
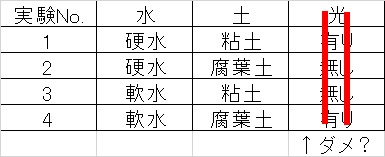
以下が最もシンプルな直交表(22型直交表)になります。
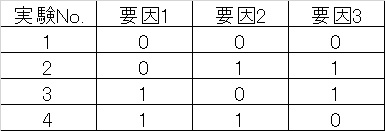
例えば先ほどの植物の生育具合の場合、以下のように割りつけることが出来ます。
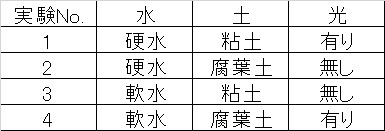
先述したように本来なら3要因2水準の実験は、総当たりで実施する場合実験を8回する必要があるのですが、この直交表を適用すると4回だけで十分という事になります。
8回から4回ではありがたみが湧きづらいですが、より拡張して7要因2水準で考えた場合は23型直交表を適用する事が出来ます。
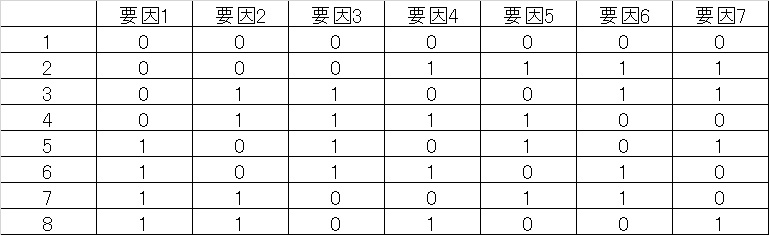
本来なら27=128回の実験が必要なところ、直交表を使う事でたったの8回の実験で十分になります。
これは極めて劇的です。
この直交表における実験結果の分析には、分散分析を用います。
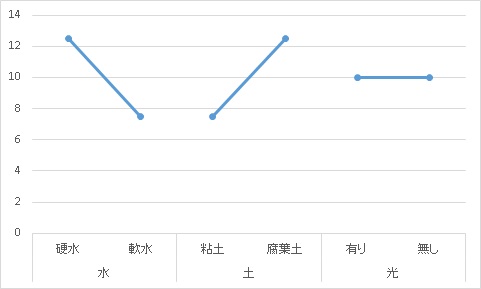
例えば、
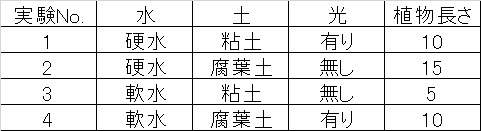
このように各実験から4つの植物長さというアウトプットが得られるわけですが、
水の効果を知りたい場合
硬水の平均値(10+15)/2=12.5 vs 軟水の平均値(5+10)/2=7.5
を分析し、
土の効果を知りたい場合
粘土の平均値(10+5)/2=7.5 vs 腐葉土の平均値(15+10)/2=12.5
を分析する事になります。
これ以降の分析方法に関しては以下の記事を参照してください。
なぜ直交表で実験回数が減るの?
それではなぜ、直交表を使う事で実験回数が減るのでしょうか。
それは調べたい要因以外は全ての要因が含まれている為です。
少し分かりづらいので、以下の表をご覧ください。
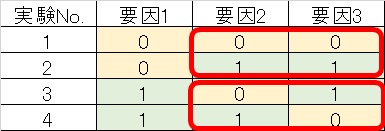
要因1に注目して1,2の平均と3,4の平均を比較するとします。
これを実施するためには、他の要因2と要因3の条件は揃っていなければ正しく比較する事は出来ません。
この直交表では実験1,2で注目すると要因2,3には0と1が2つずつ配置されており、実験3,4で注目しても要因2,3には0と1が2つずつ配置されています。
つまり、要因1以外の条件は全て等しいのです。故に要因1の各水準の平均値を比較しても、他の要因で偏る事は無いのです。
これは要因2に注目した場合も同様です。
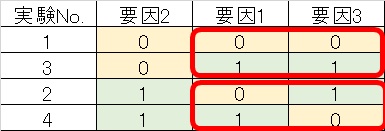
分かりやすいように実験No.を入れ替えています。やはり他の要因1,3においては全ての水準が含まれていることが見て取れると思います。
直交表はこのように、見たい要因以外は全ての同じ条件になるように組み立てられています。
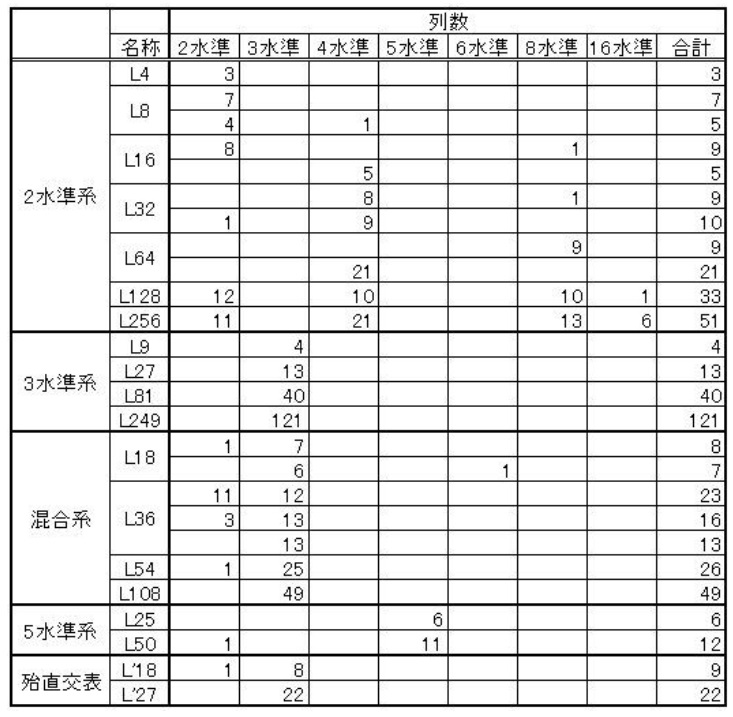
そして、直交表は様々な要因数、水準数に対応するべく既に構築されたものが取り揃えられています。
直交表を使う上で気を付けるべき点
直交表にはいくつか注意点があります。
水準数が限られる
用意されている直交表は2水準か3水準がほとんどです。
例外もありますし、複数の要因をつなげてより多くの水準数を割りつける事も出来ますが、実験回数が膨大になったり、試せる要因数が減るなど取り回しが悪くなります。
直交表での実験は飽くまで、効果的な要因を見つけるためのものとして捉えるべきです。
水準は出来るだけ大きく振りましょう。
例えば温度に注目するなら、10,20,30℃とするのではなく、0℃ vs 100℃として分散分析で有意差が出れば、温度は効果のある要因であると判断して、その後に10,20,30・・・とリニアに振って傾向を更に深堀するべきです。
そういった使い方をしましょう。
割り付けにルールがある
直交表をより正確に使うなら、実はすべての要因の列を埋めてはいけません。
先の22型直交表の場合、要因3の場所は交互作用もしくは誤差を見るために開けておくべきと言われています。
詳細は別の記事で書く予定ですが、実際のところそれほど気にしなくても、結果に大きな影響はありません。
というより、何よりもスピードが重視される昨今、せっかく使えそうな実験枠をわざわざ誤差の為に空けるなんてもったいないのです。
要因3に要因を割りつけた場合、そこには1,2の交互作用が混じってきます。
また繰り返しがない実験をした場合、誤差も拾えなくなります。
しかしながら、本来交互作用というものは単要因の作用にくらべれば小さいことが一般的です(その証拠に運用法としても交互作用にするか誤差にするか選ぶことが出来ます)
ゆえに要因3に効果がありとなった場合、交互作用が上乗せされたから効果が出たという誤判定になる確率はあまり高くありません。
それに、もし心配なら寄与率から誤差を抜いてみたり、要因1,2の組み合わせに明らかに交互作用が無さそうな要因を選んだりやりようはいくらでもあります。
また、誤差に関して言えば、繰り返して測定すれば良いだけです。
実際には100種のパターンを1回ずつ測定するよりも、10種のパターンを10回繰り返し測定する方が精度は後者の方が極めて高いです。
ちなみに、交互作用や誤差の列を使って実験回数を増やす方法は交絡法、混合法と呼ばれる立派に認められた手法ですので、ご安心ください。
とりあえず、直交表を使いたいならまずは、すべての列に要因を割りつけて繰り返し実験してデータを取ってみて下さい。
十分効果的であるという事がすぐに分かって頂けると思います。
まとめ
直交表と分散分析を利用した実験は極めて効率的です。
しかしながら、文献を見ると割りつけ方法だとか、多変量解析がどうとかで正しく実行できるのか不安にさせる情報があふれています(私にはそう思えます)。
しかし実際に使ってみると、ものすごく便利だし、思ったよりは簡単です。
とりあえず、失敗してもいいやと思って使ってみて下さい。
様々な情報が得られると思います。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント
本文中に、”繰り返しがない実験をした場合、誤差も拾えなくなります。”とありますが、これはたとえばL4直交表のすべての列に因子を割り付けて誤差列を確保しなかった場合のことを言及されていますでしょうか。
であれば、L4の4回実験を2セット繰り返せば誤差を拾えて、誤差列を確保していなくても分散分析を実施できる?ということなのか、ちょっと混乱してしまったのでご教示いただけますとありがたいです。
[…] このコンジョイントカードを作る際に、“直交表”というものが役立ちます。商品・サービスの属性や水準(例:PCの重量⇒1kg、2kg、等)を増やしていくと、組み合わせが膨大となりコンジョイントカードもものすごい数になります。直交表はこの組み合わせの数を劇的に減らしてくれるという優れモノです。直交表自体の説明もたくさんネットに出ていますので、1つだけリンクを貼らせていただきます(シグマアイ様記事)。 […]