パス図の見方

数学、理科、社会、英語、国語の5教科の関係を考えます。

仮定として

・数学、理科の能力は「理系能力」、社会、英語、国語の能力は「文系能力」が影響する

・理系能力と文系能力はある相関性がある

とすると、この関係をパス図で表すと以下のようになります。

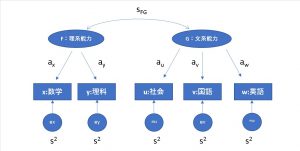
一方方向の矢印→は因果関係を示します。この場合理系能力が数学もしくは理科に影響を及ぼすということを示しています。a_x・・・は影響力を示し回帰方程式の場合、回帰係数に相当します。

両方向の矢印⇔は相関関係を示します。S_FGは相関性を示す共分散を記入します。

e_x・・・は誤差を示します。数学の点数は理系能力以外の体調や記憶能力など不特定多数の影響も受けるため、必ず誤差をつける必要があるのです。誤差を示す変数は円で囲みます。そしてその近くに分散s²を記入します。

観測されるデータは観測変量といい、四角で囲みます。この場合数学、理科、社会、英語、国語が観測変数に相当します。

多変量解析では、観測変数以外に、観測されない潜在変数というものも想定します。ここでは理系能力、文系能力が相当し、楕円で囲みます。

この潜在変数は因子分析や共分散構造分析で重要になってくる変数となります。

このパス図の「x:数学」回りの情報を読み解くと

$$x=(a_xF+c)+e$$

という関係が内包されているという事になります。

このように、パス図で表すと一見分かりづらい変数同士の関係性が一目で分かるようになります。