先日「正規分布　特性と応用」という本を購入しました。

と言いますのも統計学においては、データが正規分布であるか否か(正規性)が重要であるのに対して、正規性を論じた本を見かけないからです。

シャピロ-ウィルク検定

歪度 尖度による検定

q-qプロット

これらは名前だけは見かけるのですが、どのような検定なのかを触れた書籍はなく、ネット上でちらほら見かけるだけです。

本を読み始めた感想

これらについて言及してある書籍としてこの「正規分布　特性と応用」を購入したのですが・・・

無茶苦茶難しい・・・

とても3流大学で適当に学生をやった人間が読めるものではありません・・・。

本の内容のレベルが数式が多く難しいところもあるのですが、それ以上に正規性の分析の考え方そのものも難しいです。

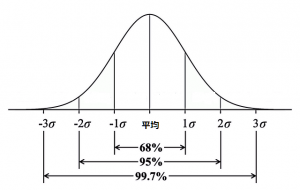
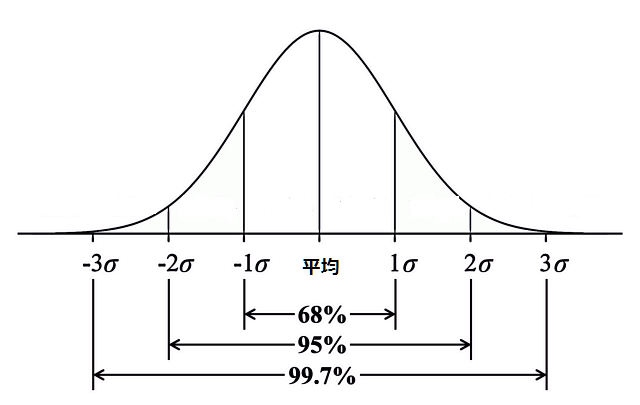
歪度-尖度による検定は、正規分布の歪みや尖り方を基準にして検定していると考えるとイメージが付きやすいですが、Q-Qプロットになると正規確率紙を応用したものであるとして、少し「？」になってきますし、正規性の検定で最も目にする「シャピロ-ウィルク検定」になると順序統計量の期待値や行列まで絡んできて、一体その数式を用いてなぜ正規性が分析出来るのか全くイメージ出来る代物ではなくなってきます。

数式もかなりややこしく、エクセルで導くのも相当に難しいものとなっています。

一応それぞれの検定における附表が当該の本には付属されていますが、それもN=50程度まででそれ以上のサンプルサイズが対象になると手に負えません。

このことを考えると「R」というものの必要性を痛感します。

「R」であれば、シャピロ-ウィルク検定も簡単なコード入力であっと言う間に分析出来るようです。

私は「R」を勉強したことがないですし、今までも別に必要ないかなと思ってはいたのですが、どうにも正規性の検定をするなら必要になりそうです。

これから「R」を勉強して紹介出来ることがあったらそれらも記事にしていきたいと思います。

正規性の検定がメジャーではない理由

今回専門書に触れてみて改めて正規性の検定が

「難しすぎる」

ということを痛感しました。

手計算では当然出来ないにしても、エクセルでもデフォルトの分析ツールでは無理であり、扱いが難しそうな「R」を使うか、有料のソフトを使用するしか対応できないとなれば、これは確かに流行らないし

「とりあえず、正規性が確保されているとして」

お茶を濁すのも無理のない話です。

でも統計に真剣に取り組みだすと、やはり正規性がちゃんとしているかということは疑問になってしまいます。

統計学の分析手法のほとんどの前提として「母集団が正規分布である場合」となっていますから。

出来れば統計に携わっている大学の先生方には、正規性に関しての簡便な書籍なり情報なりをもっと配信してほしいものではあります。サラリーマン向けに。需要はあると思うので。

私も微力ながらせめて、正規性の検定を道具としてぐらいの使い方を紹介できるよう勉強するつもりです。

あまり期待せずお待ちください。