通常売上とか、スペックなんかは一つの因子に依存するという事はありません。
そんなに世の中都合が良いわけではない。
大抵、複数の因子が一つの目的変数に影響を与えています。
それを解き明かすのが、重回帰分析です。
- 投稿が見つかりません。
エクセルの分析ツールを使うことで、データを揃えただけで重回帰分析を行うことが可能です。
しかしながら、単に与えられたデータを重回帰分析するだけでは、分からないことがあります。
それは
変量の影響力
です。
どの説明変数が、どの程度目的変数に影響を与えているのか。
これが分かれば、重要な因子にだけ力を注げば良いので、効率的に対応出来ますよね?
という事で、今回はとある工夫をする事で、変量の影響力を比較する方法を紹介します。
変量の影響力を考える

そのまま重回帰を行うと?
重回帰分析の一般式を見てみましょう
$$z=ax+by+・・・+c$$
このように、目的変数zをx、y・・・と複数の変量で説明する式なのですが、このxやyはzに対して同等の影響力を持っている訳ではありません。
当然偏りがあります。
例えば、以下のような重回帰式の場合を考えてみましょう。
$$z=0.5x+0.1y+c$$
このような場合、xは1上がるごとにzは0.5上がるのに対して、
yが1上がっても、zは0.1しか上がりません。
このように、変数の係数の大きさは、zつまり目的変数への影響力を示しています。
このようなa,bといった変数を偏回帰係数と言います。
なので、重回帰式を作った段階で、この偏回帰係数を確認すれば、説明変数の重要度が見えてきます。
よっしゃ、これで今日の話はオシマイっ!
とはなりません。残念ながらね。もう少しお付き合いいただきますよ。
この偏回帰係数を、通常そのまま捉えるとエラい事になります。
なぜならば、説明変数によってスケールが異なるからです。
例えば説明変数をそれぞれ身長xと体重yとした場合、基本的には身長は3桁で体重は2桁です。
桁数が違う変数を同列で扱えば、そりゃ目的変数zへの影響が違ってくるのは当たり前。
つまり、各変数を同列に扱えて初めて、偏回帰係数を影響度の指数として扱うことが出来るのです。
データを標準化しよう。
先述したように、偏回帰係数を影響度の指数として扱うためには、変数を同列の値として使えるようにならなければなりません。
統計学には、そのような場合に扱える便利な処理が存在します。
その方法は、データの標準化です。
$$x’=\frac{x-\overline{x}}{s}$$
この処理を行うと、例えばその数字が正規分布をしている場合、どのような正規分布であろうとも、N(0,1)の標準正規分布に変換することが出来ます。
つまり、同じスケールのデータ群として身長と体重を同列に扱ったりすることが出来るという事です。
この処理をして、重回帰式を作れば、偏回帰係数を比較する事で、データの影響を知ることが出来ます。
これだと、おそらくピンと来ないと思うので、実際にやってみましょう。
試しに計算してみよう
実際に計算してみましょう。
以下の表を元に、婚姻率を目的変数、人口、旅券発行(パスポート)を説明変数として、重回帰式を作ろうと思います。
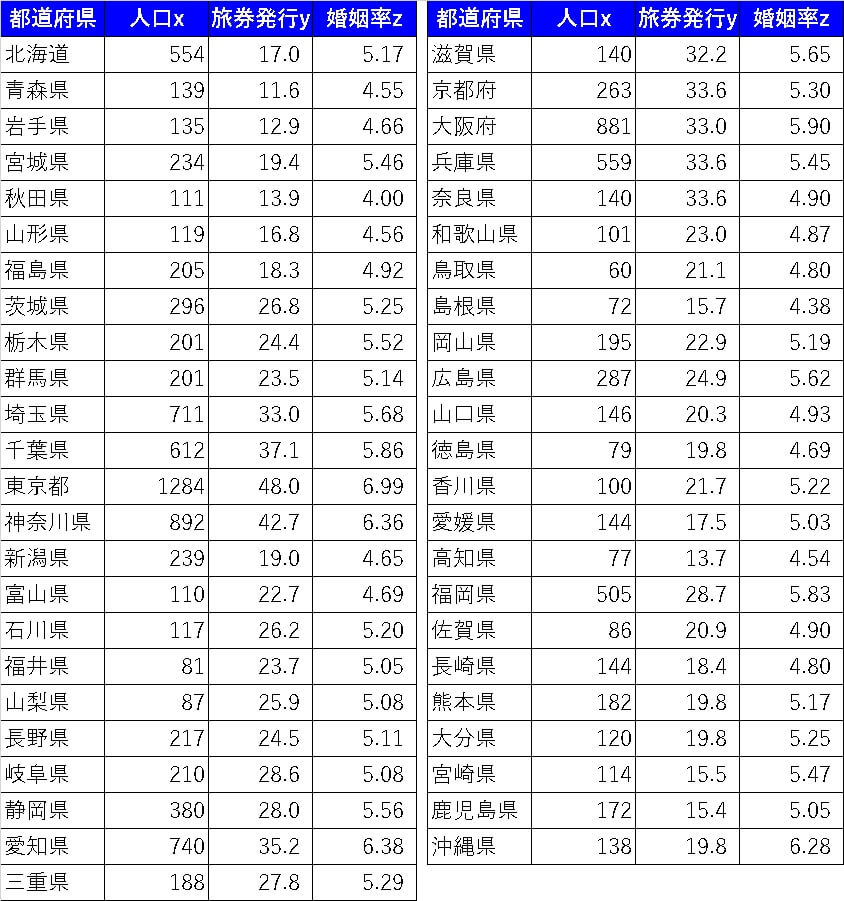
まずそのまま標準化せずに、重回帰式を作ろとこのようになります。
$$婚姻率=0.000968×人口+0.030226×旅券発行+4.231009$$
となります。以下の記事で算出していますので、よろしかったら見て下さい。
- 投稿が見つかりません。
算術したように、ここで係数に注目すると、旅券発行の方が影響度が高いように見えます。
しかしながら、数字のスケールが全然違うので、単純に比較は出来ないのです。
という事で次は、説明変数である人口、旅券発行を標準化します。
例えば北海道の人口554の場合、
人口の平均値:271.66
人口の標準偏差:263.77
なので、
$$\frac{554-271.66}{263.77}=1.07$$
となります。このような具合ですべての値に標準化処理を施すと
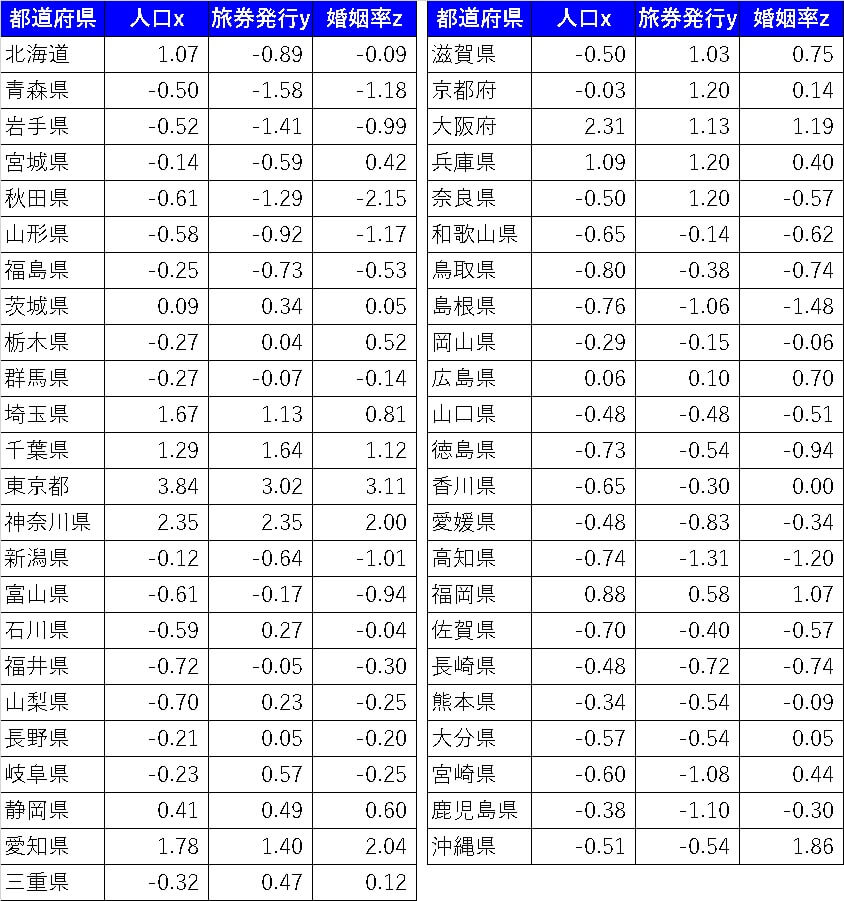
このようになります。
あとは同じようにエクセルの分析ツールで回帰分析を行うと
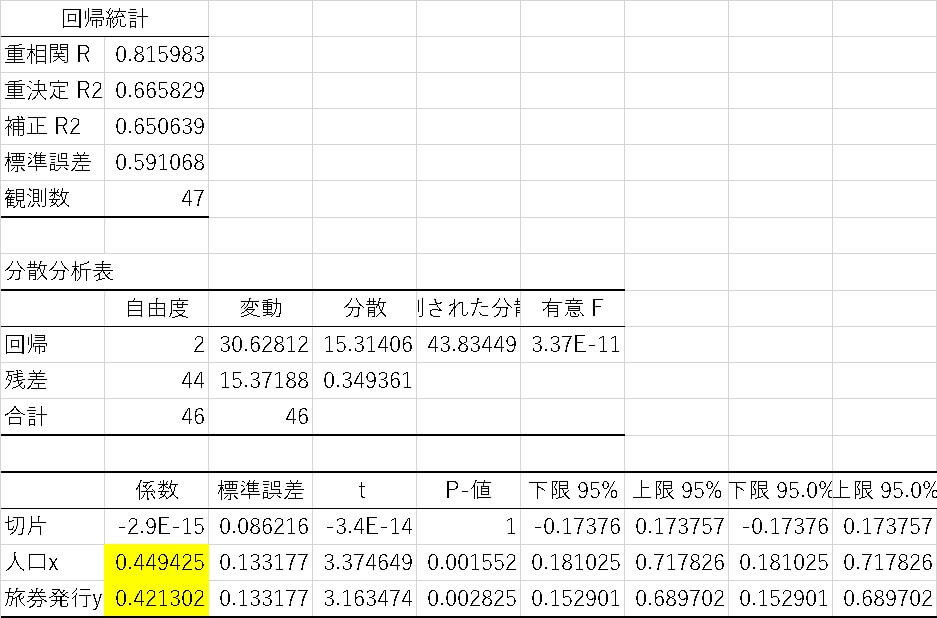
このような結果になります。
標準化前の重回帰式では、旅券発行の方が係数が大きかったのですが、実際に標準化してから計算すると、ほぼ人口と旅券発行は同程度の影響度であることが分かりました。
このように、標準化することで変量の影響力を簡単に見える化することが出来ます。
標準化もエクセルの関数で簡単に導けます。
売上、利益などにどの要素がより大きな影響を与えているかを調べるときに、ぜひ標準化と重回帰分析を使ってみてください。
まとめ
重回帰を使うと、複数の変数がどのように影響しあって説明変数に繋がっているのか見えるようになります。
しかしながら、説明変数をそのまま使って重回帰式を作ると、桁数の違いなどで係数の違いがそのまま影響度を表すとは限らなくなります。
そのため、標準化の処理をしてから重回帰をするようにしましょう。
簡単でありながら、そこから得られる情報は非常に価値の高いものになりますよ。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント