以前紹介した箱ひげ図(ボックスプロット)は分布同士を比較出来る、非常に有用なツールです。
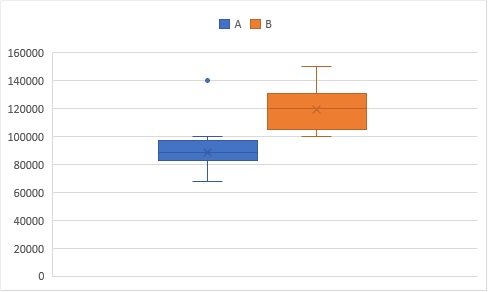
・中央値と平均値のズレ(=分布の中央のズレ)
・箱のサイズによるばらつきの比較
・外れ値の有無
等々、豊富な情報を1枚で提供してくれます。
しかし、私個人としては一つ気がかりな事があるのです。
それは
何%外れた値を外れ値にしてんの?
ということです。
この情報、実はネットで検索したり、本を読んだりしても引っ掛からないのです。
少なくとも私は探し当てることが出来ませんでした。
このような状態では、もし上司が箱ひげ図を知らない場合
「この外れ値って何%の確率で発生するの?」
と質問されると言い淀んでしまいます。
折角良いデータになったとしても、これでは却下されてしまいます。
箱ひげ図の代用となるグラフは中々思いつかないので、これでは困ってしまいます。
ということで、今回は箱ひげ図を標準正規分布表と比較することで、外れ値の発生確率を算出してみました。
結論としては、なんと3σとほぼ同等という結果になったのです。
このような情報が有るのと無いとでは、やはり説得力の重みが大分違ってきます。
それでは、いかにして3σと一致したのか一緒に紐解いていきましょう。
箱ひげ図(ボックスプロット)の外れ値の確率を算出しよう

箱ひげ図のおさらい
箱ひげ図の箱は値を小さい順に並べたときの、下から25%の位置(第一四分位値)から75%(第三四分位値)までの位置の長さに相当します。
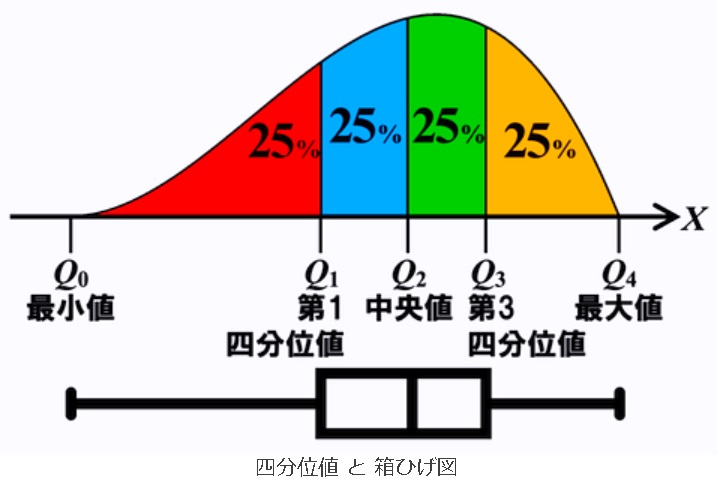
つまり箱の中央からプラス方向とマイナス方向に25%ズレた位置が箱のサイズとなるのです。
これが今回のミソになります。
標準正規分布と箱ひげ図を重ねてみよう
例えば標準正規分布を、箱ひげ図に置き換えるとどのようになるでしょう。
・中央値が正規分布の中心(=平均値)と一致します。
・第三四分位値は右側に25%の値が収まるZσと一致します(第一四分位値は左側)
以下のようなイメージを持つと分かりやすいと思います。
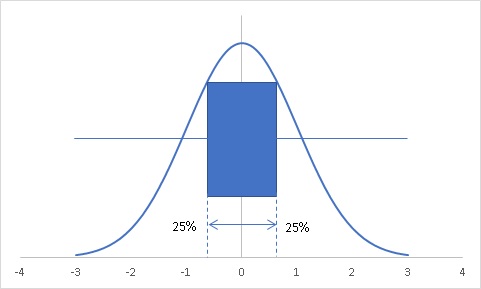
ここで、標準正規分布表の出番です。
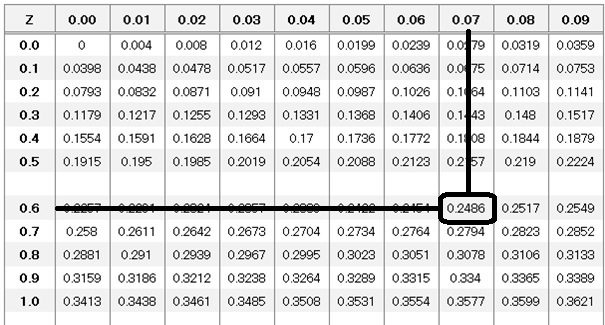
とりあえず、片側だけで考えていきます。
正負いずれも同じことですから。
表の25%(つまり0.25)に相当するz値を探ります。
z=0.67か0.68ってところですね。
とりあえず小さめの確率である0.67を選んでおきます。
つまり0.67σが第三四分位値と第一四分位値にほぼ一致するという訳になります。
四分位+1.5×IQRの確率は?
外れ値は
$$75\%点(25\%点)+(-)1.5×IQR$$
より外側の値と箱ひげ図では定義しています。
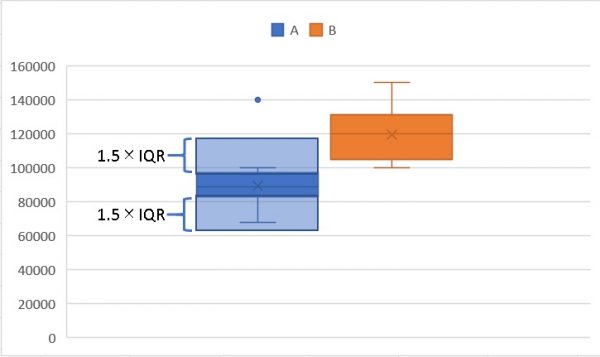
IQRとは箱のサイズです。
まず先述の確認結果から75%を0.67になります。
次にIQRを算出しましょう。
25%~75%点までの長さなので、0.67の2倍1.34がIQRになります。
$$IQR=0.67×2=1.34$$
よって外れ値にならない領域は
$$z=75\%点(25\%点)+(-)1.5×IQR=0.67+1.5×1.34=2.67$$
となります。
つまり±2.67σが、箱ひげ図が表す通常の分布範囲ということになります。
先述したように3σに近い値となっています。
外れ値が発生する確率は?
それでは最後に外れ値が発生する確率を算出しましょう。
Z=2.67に相当する確率を標準正規分布表で確認しましょう。
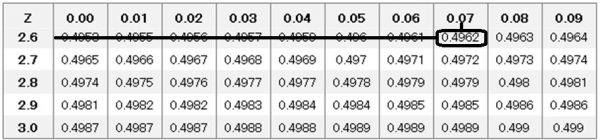
結果としては、0.4962(≒49.6%)になります。
これを両側に拡張すると、
$$49.6\%×2=99.2\%$$
となります。
±3σの範囲に入る確率が99.7%であることを考えると、その差はわずか0.5%!
2.67σという値は、思った以上に3σに近いものだと分かって頂けたはずです。
2.67σと最初に見たときに
「3σと全然違うじゃん」
と思ったあなた!これで勘弁してください・・・
まとめ
以上の結果から正規分布である場合、箱ひげ図における外れ値とは0.8%(100%-99.2%)の確率でしか発生しない稀なデータのことを指すということが分かりました。
個人的には精々5%から外れた時くらいだろうと思っていたので、この結果には驚きました。
ほぼ3σなんですね。早とちりして上司に適当なことを吹き込まなくて良かったです。
ただし注意しなければならないのは、この結果は飽くまでデータが正規分布に従っている場合に限るという事です。
この世には色々な分布がありますし、正規分布に似ていても歪んでいたり、尖っていたり様々です。
なのでこの値は目安として扱う程度に留めておいてください。
ただこういう統計グラフを見る際に目安を知っているというのは、かなり大きな武器です。
「箱ひげ図って何%の確率で外れ値が出るの?」
と聞かれた場合、
A「かなり低い確率だよ」
B「正規分布のときに1%以下だから、かなり低い確率だよ」
いずれの場合の方が、説得力を有するか一目瞭然です。
何かを説明するとき、特に統計の知識に関する場合は数字を絡めるようにして伝えることで、高い理解度を持っているとアピール出来ますし、説得力も段違いです。
おそらく箱ひげ図をここまで理解して、使いこなしている人は殆どいないはずで、この記事を読んだあなたはかなり貴重な人材となっているはずです。
皆さんも箱ひげ図に関して、質問されたときにこの値 99.2% を使ってみてください。
統計が得意アピールが出来ますよ!
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント