こんにちは、熊野コミチです。
皆さん、品質工学使ってますか?
私自身実用にチャレンジし始めて2年ほど経過したのですが、やればやるほどに製品開発には必須の概念、手法であると日々痛感しております。
当ブログをはじめ、私のコンテンツでは統計学を中心に扱っていますが製品開発や品質管理といったメーカーにおけるデータ測定と解析が必要な部署において、品質工学の概念を理解している/していないとでは同じ統計学を使うにしても解析効率、実験効率に雲泥の差が生じます。
そういった意味でも、品質工学はぜひ全ての技術者に知ってほしいスキル。
しかしながら品質工学を使っている人は殆どいません。
少なくとも私は職場で見たことが無い(私がもっぱら普及する側)。
理由としては明確です。難しいんです。
というより
なぜそのようなやり方をしないといけないのか理解出来ないんです。例えば
「動特性でデータを取らなくてはいけない」
と言われたら
「なんで?」
って言いたくなるのが人情ですが、そんな痒い所に手が届く形の回答をくれないのです。
少なくとも一般的な品質工学のテキストでは全く見かけられない。納得できない。
理解出来ないのですから、使われない。そんな悪循環を生じています。
という訳で今回はそんな品質工学でも、なんでそんな風にしないといけないのか分からないもの第一位である動特性の解説をしたいと思います。
私自身動特性出ないといけない理由が長らく分からなかったし、今でも自確信は無いのですが無理矢理実用していくうちに、なんとなくは理解出来てきました。
多分この記事を読んでくだされば、動特性でデータを取ることがいかに効率的か分かって頂けるとモノと思います。
動特性とは?
特性を働きでみる
まず簡単に動特性そのものの説明をします。
動特性は読んで字のごとく、動く特性を指します。
例えば扇風機で考えてみます。
扇風機は風を起こして涼を取るための装置ですが、今時風の強さが一段階しかないものって見かけないですよね。
少なくとも弱、中、強はある。
この3段階は流す電力の強さに比例します。
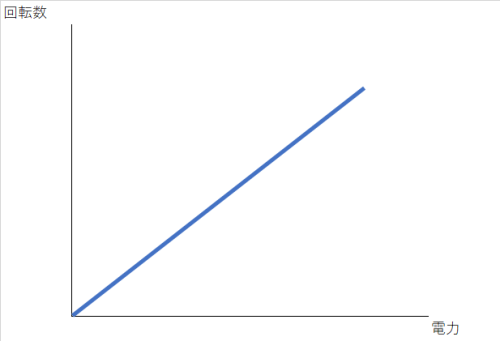
このように入力と出力の関係性で見る方法を動特性と言います。
ちなみに、単一の入力で風量を見る場合は静特性と言います。
品質工学においては、原則動特性で評価することが望ましいとされています。
しかしやってみると分かるのですが、いざ自分の製品を動特性で表現しろと言われるとかなり難しい。
一定の慣れが必要です。
ちなみに動特性の事例集として私のnoteでは、品質工学の論文紹介をしています。
またこちらの書籍でも動特性のアイデアを紹介しています。
もし動特性が思いつかない場合は上記のサイトや書籍を読んで頂けますと、思いつきやすくなると思います。
動特性って必要なの?
自分の製品の動特性は中々思いつきづらいのですが、そもそも動特性にこだわる必要はあるのでしょうか?
品質工学には、従来扱ってきたような品質特性に該当する静特性による評価方法も提案されていますし。
別にいらんくね?
ってなると思います。
という事で、ここからが本題の動特性でデータを測定する必要性、利便性を解説していきたいと思います。
なぜ動特性が必要なのか?
少ないサンプルサイズでOK
動特性でデータを取ることで、必要以上にデータを測定する必要がなくなります。
スピードが求められない仕事は原則存在しませんから、データ測定の手間が省けるのは大変喜ばしい事です。
その理由を解説するために、まず以下のシチュエーションを例に考えてみましょう。
先ほどと同様に扇風機で考えてみます。
扇風機の回転数を測定する場合、通常ならどうしますか?
多分一定の電力を流して、回転数を測定すると思います。
そして同じ電力でも毎回様々なばらつきがあると思いますから、ちょっとずつ回転数もばらつきます。
となれば、正確な回転数を測定するには何回も測定する必要が出てきますね。

統計学に明るい方なら、正確なばらつきの範囲を把握するにはn=30は欲しいなと考えるはずです。
何を測定するにしても、30回も何かを繰り返すというのは大変なものです。
一事が万事、全てにおいてこのようなデータの取り方をしていたら、データの解釈をするまでの時間が長くなり必然アクションの回数が減ってしまいます。
対して動特性でデータを取るとどうなるかというと、こうなります。
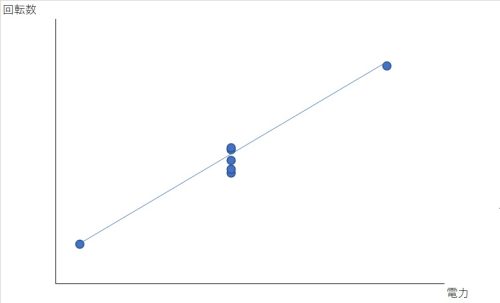
ここで重要なのが、電力(信号因子)を十分に大きく振っていれば真ん中の回転数が最大の電力時の回転数よりは小さいだろうし、最小の電力時の回転数よりは大きいという事が予測出来るという事です。
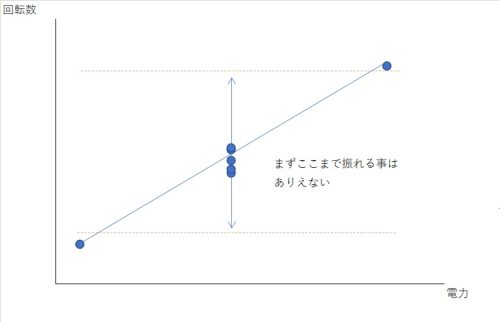
また、電力と回転数のような入出力の関係が出来ていれば線形のグラフになるはずです。
つまり、そのようなグラフにならない場合は測定ミスによる外れ値の可能性を察する事が出来ます。
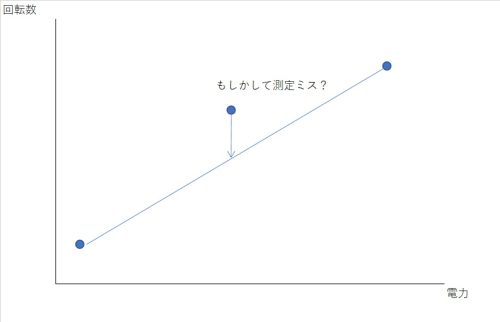
つまりたったの3点のデータで、
・データがばらつき得る範囲
・外れ値の検知
が可能となるわけです。静特性の場合は3点でこれだけの情報を得ることが出来ません。
誤差因子の効果を判定しやすい。
更に言えば、誤差因子と想定したものが本当に誤差因子なのかも判定しやすくなります。
誤差因子とは設計者が制御出来ないノイズを指します。
例えば電池というものは、20度前後の常温であれば問題なく作動しますが、寒い環境下だと化学反応がうまく進まずすぐに使えなくなってしまいます。
このような電池に対する気温が誤差因子に該当します。
品質工学においては、こういった誤差因子下においても動作効率が落ちないかどうかを検証することを推奨しています(これが機能性評価と呼ばれるものです)。
そしてこの誤差因子がうまく設定出来るかという事も、動特性の案出しと同じくらい難しく、技術者の腕の見せ所になるわけなのですが、静特性で見つけるより動特性で見つけるほうが間違いが少ないです。
扇風機の例で説明します。
誤差因子としては、気温が高くなることで配線の抵抗値が上がって回転しにくくなることを想定したとします。
静特性で、この誤差因子が本当に誤差因子として使えるかを確認した場合、こんなデータになる可能性があります。

低温によって差が生じているようにも見えますが、どうにも不明瞭です。
3σのレンジを伸ばすと、有意差が無いかもしれません。
さてこの問題、動特性の場合はこんなデータになる可能性が高いです。
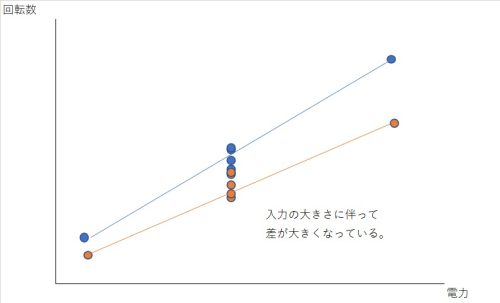
入出力が正しくエネルギーの関係であれば、入力の増加に伴って誤差因子の影響も大きくなっていきます(この関係性で動特性であるかどうかを見極めたりもします)。
つまり小さい入力では本当に誤差因子かどうか分からなかったものも、入力を大きくしていくことで本当に測定ばらつきよりも阻害効果が大きいか見極めることが出来ます。
今回の事例では中程度の入力で示しましたが、あなたが今現在測定しているものの入力が中程度かどうかは分かりません。
もし弱レベルの入力で合った場合、誤差因子の効果は完全に測定誤差に飲み込まれるでしょうから誤差因子の選定を誤ったり、実験の再現性が取れなくなる可能性が高くなります。
実は統計学にも応用できる考え方
実はこの動特性の考え方は統計的なデータを取る際にも有効です。
例えば何かの粘着力を測定するとします。
通常ならば、温度を一定にした部屋で測定すると思います。
粘着剤の柔らかさは一般的には温度によって変わるので、温度管理されていないところで測定すると大きくばらついてしまうからです。
ですがここで、先ほどの動特性の考え方を適用するとあんまりシビアに構える必要がなくなります。
温度差でばらつくのであれば、温度を大きく振ってあげれば良いのです。
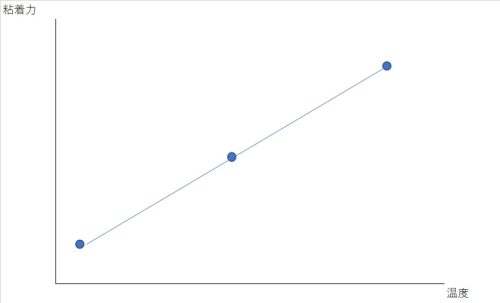
このようにして測定したデータで回帰分析をすれば、常温の真値だけでなく各温度における粘着力もおおよそ予測することが出来るようになります。
この例でいう温度のような「ここが振れたら測定値がぶれるだろう」という点を逆手に取ってやることで、データの精度と情報量を同時に確保することが出来るのです。
そもそも以前私が受けたセミナーでは、日本人はビッグデータの認識を誤っているという指摘をしていました。
日本においてはデータの正確性を重視して、何回も繰り返して測定することを推奨しがちであると。
先ほどの粘着性でいうと、常温における粘着力は~Nなのか。その値は何回測定しても再現するか。ここを重要視していると。
ですが本来のビッグデータは、どれだけ広い範囲のデータを測定出来ているか重要なんです。
つまり常温だけでなく、低温も高温も測定する。それぞれの温度のデータは別にN=1でも良いと。
ビッグデータのビッグとは、深さではなく広さを指しているという事です。
今回紹介した動特性の概念と利便性からも、実はデータ測定においてはいかに広くデータを測定することが重要かがよく分ります。
あなたもぜひ、これを機に動特性でデータを取る癖を身に着け、広くデータを測定し仕事のスピードアップをはかってください。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
また最近は私が実務で多用していることもあって品質工学の解説も始めました。
「いや、品質工学勉強したことがあるけど、機能?とかよく分らなくて結局使ってない」
そんな方向けにnoteで品質工学の論文を分かりやすく解説しています。
品質工学を使いこなすには、実用が一番なのですが、教科書⇒実用というのはどうにもハードルが高い。
そのハードルを低くするには、過去論文を読んで様々な機能の考え方に触れるのが一番なんです。
こんな感じで、様々なコンテンツを展開しています。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント