統計学には、数多くの分析手法が存在します。
標準偏差を始めとした、統計量
データ群の比較をする検定
真の値を予測する推定
データを見える化する、グラフたち
覚えたての状態で、これらの手法を使う際に犯してしまいがちな間違い。
それが、単一の手法でデータを分析してしまう事です。
データ分析は単一の手法だけで行うと、必ず失敗します。
なしてか?
今回は、単一の手法でなぜダメなのか、そして2つのデータを比較するときの複数の手法の併用例として、t検定と箱ひげ図の併用を紹介します。
動画でも解説しています。
単一の分析手法のみで分析してはいけない?

データの分析は、情報を単純化する作業
そもそもデータを分析するって事を考えてみましょう。
生のデータには、様々な情報がごった返しています。
人間というものは、複雑なものを理解するというのがとても苦手です。
生データは情報が複雑すぎて、そのままだと人間には理解が出来ないのです。
故に、まずはデータを分解して、単純な要素を取り出してあげる必要があるのです。
平均値というものは、様々なばらつきの要素を取り除いて、データ群の中心に位置する情報を抜き出したものです。
標準偏差は各データが中心の値から、どれだけばらついているかだけを取り出したものです。
正規分布は、平均値と標準偏差のみから分布の形を近似したものです。
以上のような手法は、生データから余計な情報を取り除いたものになります。
いらないものを取り除いているために、とても比較がしやすいのです。
分析とは、情報を捨てているのと同義
しかしながら、逆を言えば、各代表値や分析した結果は情報が抜け落ちているとも言えます。
平均値同士の比較では、ばらつきの情報が分かりません。
標準偏差同士の比較なら、中心値の情報が分かりません。
平均値と標準偏差が同じなら、多少の違いがあるはずの2つの分布の区別は全くつかないでしょう。
このように、分析手法は分かりやすくするために、ある種データを捨てているので、単一の手法だけでは、そのデータの一面しか見る事が出来ないのです。
故に一つの手法ではなく、複数の手法を駆使する事で、様々な角度でデータを観察して、初めて生データの全容を知ることが出来るようになるのです。
t検定と箱ひげ図

2群のデータの比較における、おススメの組み合わせ
ということで、データの分析には単一手法だと、一面しかとらえられず、あきまへんわという訳なのですが、なら
「どの組み合わせで使えば良いんですか(怒)?」
と、当然なるわけです。
とりあえず、今回紹介しますのは、t検定と箱ひげ図の組み合わせです。
箱ひげ図は、データの情報から中央値、四分位範囲、最大/最小値、外れ値を抽出し、まとめなおしたグラフで、分布の形を単純な箱とひげで表現したものです。
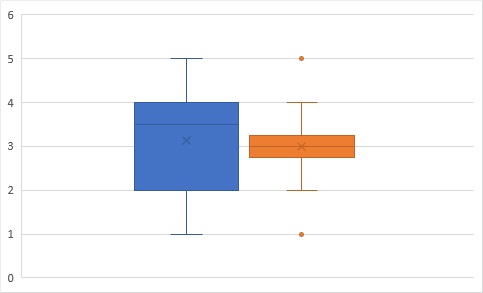
箱ひげ図の詳細は、こちらの記事を参照ください。
このグラフの利点は、分布の全容を捉える事が出来るという点です。
平均値、中央値の差はこのくらい
とか
箱のサイズ差から、ばらつきの差はこのくらい
とか、一つのグラフで非常に多くの情報を得る事が出来ます。
この時点で、おそらく分布間に差が有るかどうかを8割方見極める事が出来るでしょう。
ばらつきを考慮した上で、中心の値を比較出来ますからね。
ですが、実際に有意差があるのかどうかは、やはり目視比較では弱いです。
なので、箱ひげ図の補足として、t検定を実施するのです。
検定は補足として使おう
箱ひげ図で、分布間の関係をおおよそ掴んだら、t検定を実施します。
かつて2群の比較をt検定で行う時には、
F検定でばらつきの違いを比較
F検定の結果で、t検定の手法(通常のt検定かwelchのt検定)を決める。
という方法が主流でしたが、現在は検定の多重性の問題もあり、F検定は実施せずにwelchのt検定で検定を実施するという方法が主流となっています。
という事で、t検定は即welchのt検定で比較しましょう。
これで、平均値同士に有意差があるのかを、一定の確率の元判断する事が出来ます。
ちなみに、ここで更に検出力も分析しておくと、検定がどれだけ正確なものかを知ることが出来ます。
検定を覚えてしまうと、ついそれだけで分析をしてしまいたくなります。
有意差の有無を、確率で担保してくれるので、間違えるはずがないと思ってしまうからです。
ですが、検定は万能ではありません。
有意水準は、そのまま設定した確率(例えば有意水準α=5%)分間違えるリスクを背負っています。
その上、検出力を考慮して正しいサンプルサイズ(多すぎても少なすぎてもダメ!)で検定しないと、間違った判断になってしまいやすいです。
こういった、誤った判断を避けるためにも、グラフで全体像を把握しておく必要があるのです。
グラフ、特に箱ひげ図を眺めると、データ間に差が有るかどうかは察しがつきます。
ですが、あくまで目視判断で、もうちょっと強い担保が欲しい。
なので、検定を担保にして、
ほら差が有るでしょ(ないでしょ)?
と言い切る。
こんな使い方が、適切だと思います。
グラフで比較、検定は担保
ここを押さえておけば、データ比較でのミスは避けられると思います。
まとめ
データの分析は、一つの手法に偏ると必ず失敗します。
データ分析を正しく行うコツは、複数の手法で多角的に観察する事です。
例えば、2群のデータ比較の場合は、箱ひげ図とt検定がとても相性が良いです。
エクセルを使えば、秒で出来ますので、ぜひ活用してみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント
Great content! Super high-quality! Keep it up! 🙂