通常のt検定では、3群以上の平均値の差について有意差の有無を確認することが出来ません。
なぜなら、多重性の問題が存在するためです。
しかし、実際のところ3つ以上の平均値に関して、有意差が知りたいというシチュエーションは多いハズ。
この悩みを解消する手法が多重比較法です。
今回はそんな多重比較の中の一つテューキー法について紹介いたします。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
テューキー法とは?
全ての組み合わせを検定する多重比較法
テューキー法は、それぞれの平均値の差を比較するときによく用いられる手法です。
例えば群A1,A2,A3,A4,A5が存在する場合、
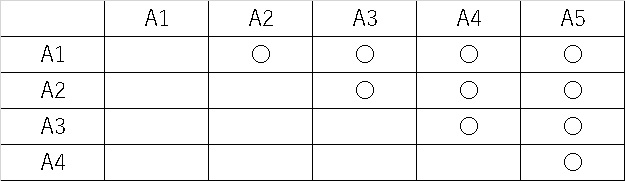
これらすべての組み合わせで検定するのに向いています。
t検定との式の違い
ここでt検定との式の違いを見てみましょう。
t検定(welchのt検定)の検定統計量tの式は
$$t=\frac{x_1-x_2}{\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}}}$$
です。一方テューキー法における検定統計量tの式は
$$t=\frac{x_1-x_2}{\sqrt{V_E(\frac{1}{n_1}+\frac{1}{n_2}})}$$
になります。ここでVEは誤差分散の値になります。
t検定では個々の群の”ばらつき”σを使用しているのに対して、テューキー法では誤差分散VEの値を使用しています。
誤差分散は、分散分析でF検定を用いる際に使用されています。
多重比較の手法が、分散分析の延長線上に存在している事がよく分かります。
基本的には、更に誤差自由度φEを算出します。
$$φ_E=N-a$$
Nは総サンプルサイズ、aは群の個数です。先ほどのA1~5の場合はa=5になります。
これらの条件からステュデント化された範囲q(a,φE;α)/√2を、検定統計量tが上回った場合有意差がある判断します。
正直な話、この多重比較に関しては、こういった概要と後程述べる注意点さえ押さえておけば良いように思います。
仕事で平均値を複数比較したいという需要を満たすのであれば、それで問題ないはずです。
それでも、興味があるという方はこちらの書籍をお勧めします。
 | 新品価格 |
多重比較の方法は考え方が網羅的に記述されており、これ一冊でカバー出来ます。
EZRで実施してみよう
実際に分析してみよう
EZRを使うことで、かなり簡単にテューキー法を用いた検定を実施することが出来ます。
今回は以下のような複数の群について、考えてみましょう。

ちなみに、このようなデータをEZRに入力する際には、
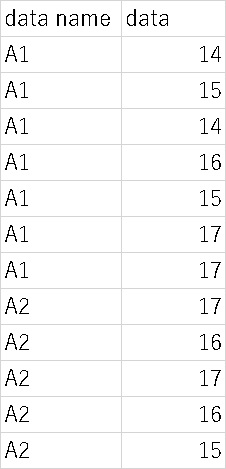
このように、縦に並べましょう。
データをEZRに入力した後、『3群以上の平均値の比較』を選んでください。
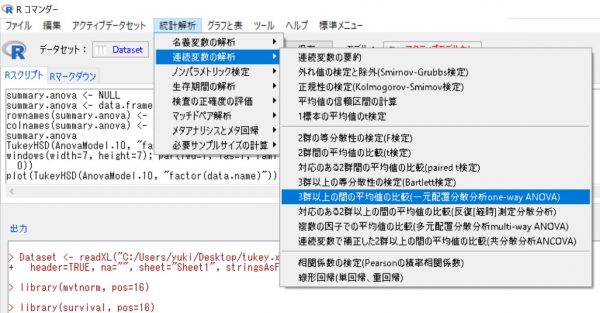
こちらを選択した後、
・比較する群には、データの名前を入れている行を選択してください。
・等分散と考えますかには、はいを選択してください(重要)。
・そして2群ずつの比較(tukey法)を選択してください。
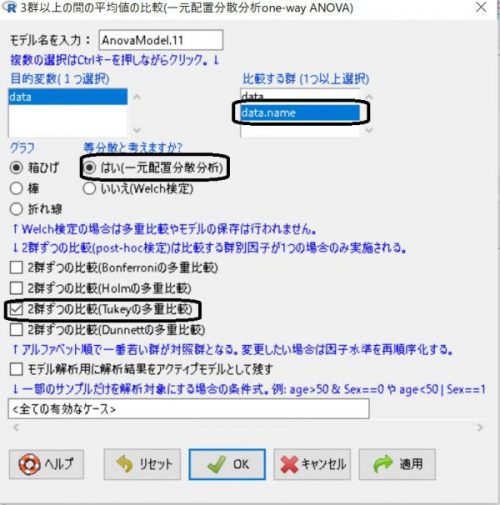
そしてOKを押せば結果が出力されます。
分析結果の見方
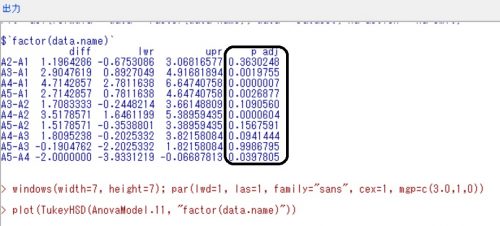
注目すべきはP値(P adj)です。この値が0.05を下回っている場合、有意差ありとなります。
例えば、A2とA1の組み合わせにおいては、P値が0.36と0.05よりも大きいため有意差なしです。
対してA3とA1に関しては0.0019と0.05を下回っているため、有意差ありになります。
このようにEZRを使うことで、簡単に複数群の平均値の検定が可能となります。
テューキー法使用の注意点
テューキー法に限った話ではなく、多重比較法全般に言えることですが、前提条件として複数の群の全ての分散(つまり”ばらつき”)が等しい必要があります。
先述した式を見て頂ければ、その原因が分かります。
$$t=\frac{x_1-x_2}{\sqrt{V_E(\frac{1}{n_1}+\frac{1}{n_2}})}$$
分母には誤差分散しかありません。
welchのt検定では分散が異なるシチュエーションに対応する為に、分母には各群のσが組み込まれていますが、テューキー法では、この分散の値が一つだけなのです。
これを考慮して、EZRでのテューキー法では、等分散と考えますかをいいえにすると、テューキー法が算出されません。
この点だけは注意してください。
まとめ
テューキー法を用いる事で、複数の平均値を同時に検定することが出来ます。
EZRを使用することで簡単に実施出来ますので、ぜひ皆さん活用してみて下さい。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント