回帰分析や相関性の分析は、基本的に関係性を線形の式に当てはめることで行います。

$$\overline{y}=a+bx$$

非線形の分析は非常に難しいためです。

ですが、実際には成長曲線のように非線形の関係についても分析しなければならない時があります。

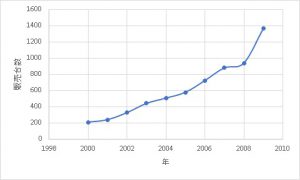
今回は成長曲線のような「指数関数」を回帰分析するためのテクニックを紹介します。

指数は対数に変換しよう

yがxの指数関数で表される場合に説明される統計モデルを対数線形モデルと呼びます。

$$\overline{y}=ab^x$$

このような関数をグラフとして図示すると先ほどのグラフのように、xの増加に伴って爆発的にyが増加するような指数曲線を描きます。

このような指数関数は非線形ですので、通常の回帰分析を適用することが出来ません。

しかしながら指数関数は対数関数に置き換えることで、線形に変形することが出来ます。

実際に式変形を見てみましょう。

まず先ほどの指数関数の両辺に自然対数を取ってみます。

$$\ln{\overline{y}}=\ln{ab^x}$$

この右辺は以下のように変形することが出来ます。

$$\ln{\overline{y}}=\ln{a}+x\ln{b}$$

この形なんか線形の式っぽくないですか？

更にこのように置き換えると

$$Y=\ln{\overline{y}}$$

$$A=\ln{a}$$

$$B=\ln{b}$$

↓

$$Y=A+Bx$$

線形の式そのものに変形出来ました。つまりxに対してYの変化をプロットすれば成長曲線のような非線形も線形の式として表すことが出来、ひいては回帰分析や相関性の分析を適用することが出来るようになります。

また対数変換して得られた回帰式を、指数関数にまた変換してあげれば元々のグラフの回帰式を見出すことが出来ます。

具体例で考えてみよう

最初に示したこちらのグラフを実際に変換してみましょう。

ちなみにこちらは、各年における車の販売台数です。実際の数字はこちらになります。

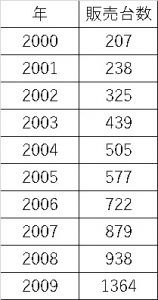
この販売台数の対数を取ります。例えば2000年の場合

$$\ln{207}=5.3$$

となります。このように各年の値を対数変換すると、

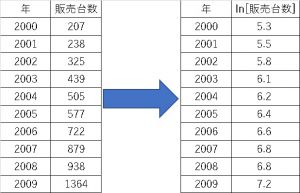
となり、こちらをプロットすると、

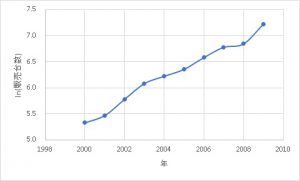
となります。変換前と比較してかなり直線に近いグラフとなっています。

こちらの線形グラフから、最小二乗法を用いてA,Bを求めた場合最終的に以下のような式が導き出せます。

$$Y=A+Bx=5.36+0.20x$$

この式を指数関数に戻すには

$$A=\ln{a}=5.36$$

↓

$$a=e^{5.36}=213.4$$

そして

$$B=\ln{b}=0.20$$

↓

$$b=e^{0.20}=1.22$$

という処理を施せばいいです。結果として最初の販売台数を示す指数関数は

$$\overline{y}=213.4×1.22x$$

という結果となります。

このように、指数関数のように非線形の関係性でも線形に変形させることで、通常の回帰式や相関性分析を適用出来るようになります。

今まで、

「非線形だから、結局使えないな」

と諦めていた人は一度試してみてください。うまくことが運ぶかもしれません。