
以前尺度には、間隔尺度、順序尺度、名義尺度に分かれると紹介しました。
間隔尺度同士、順序尺度同士は一般的な相関係数で説明出来るのですが、名義尺度同士は実は事情が異なります(順序尺度同士の場合は、スピアマンの順位相関係数ですが、これは通常の相関係数の特殊事例です)。
今回は名義尺度同士の相関性を表すクラメールの関連指数を紹介します。
名義尺度ってなに?
各都道府県の人に「あなたはどこの野球チームのファンですか」と尋ねた場合、以下のような集計結果が得られます。

この場合、巨人、阪神、広島、横浜には間隔的、順序的に序列は存在しません。
また東京、大阪、福岡も同様です。
これらを名義尺度と言います。
ピンとこない場合は、各チームを1号チーム、2号チームと言い換える、もしくは都道府県を1丁目、2丁目と言い換えるともう少し分かりやすいかもしれません。
そして、このような各都道府県とチームのファンの人数に相関があるのかをこれから考えていきます。
クロス集計表
先程の表のままだと、まずすべてのデータを表すのに当ブログの行が無くなってしまいますし、何より見づらいですので、以下のように集計します。
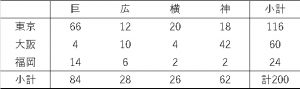
かなりすっきりしました。
このような2つの項目を縦横に集計した表をクロス集計表といいます。
クラメールの関連指数
今回はこの表の値から改めて相関を考えていきます。
ここからの相関関係の考え方ですが、
「本来の期待値からのズレの大きさ」
という観点から攻めていきます。
東京、大阪、福岡には116:60:24の割合で人が住んでいます。
また巨人、広島、横浜、阪神のファンの割合は84:28:26:62です。
ここから例えば東京には本来
$$200(調査総数)×\frac{116}{200}(東京の人の割合)×\frac{84}{200}(巨人ファンの割合)=48.72$$
という値が期待されます。このように各組合せの期待値を算出すると以下のような表になります。
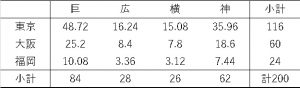
この期待値と実際の値には差があるのは、表を比べれば明白です。相関はこの実現値と期待値の差を利用して算出します。
各項目差は以下のようにあらわすことが出来ます。
$$\frac{(実現値-期待値)^2}{期待値}$$
実現値と期待値の差は偏差です。ゆえに2乗しないとその後足し合わせ処理の際に0になってしまいます。
そして期待値で2乗値を割る理由ですが、これは東京/巨人は48.72に対して、福岡/横浜は3.2と元々の期待値の重みが違うので、2乗値そのままではえこひいきになってしまうので、期待値で割ることで平等化しているのです。
このような計算をした表が以下になります。
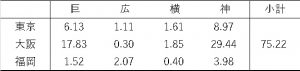
この足し合わせて算出された値75.22はカイ二乗そのものです。
$$x^2=\sum{\frac{(x-\overline{x})^2}{\overline{x}}}$$
ここまで来ればもう少しです。
このカイ二乗は、クロス集計表の行と列の数が大きくなると、自然と大きくなることが予想されます。
なので、対称の行と列の組み合わせが取り得る最大のカイ二乗で、先ほど算出したカイ二乗を割れば相関性を表した値が手に入ります。
このカイ二乗の最大値ですが、以下の式で算出されます
$$N(N_{min}-1)$$
Nはデータの全数、Nminは行と列の小さい方の値です。
例えば、今回の例では以下のような表になった場合、カイ二乗は最大の値をとります。
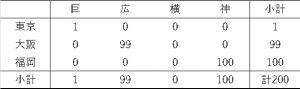
ぜひエクセルで計算してみてください。200×(3-1)=400に一致します。
最後の締めです。先刻申したようにカイ二乗の計算値と最大値の比を計算します。
$$q^2=\frac{\frac{\sum{(実測値-期待値)^2}}{期待値}}{N(N_{min}-1)}$$
このq2が名義尺度同士の相関性を表すクラメールの関連指数です。
相関係数に相当する値が欲しい場合は、q2の平方根をとりqとして扱ってください。
今回の表では
$$q=0.43$$
になります。
相関があるかは微妙なところですが、完全にないとも言い切れません。
ちなみに、今回の結果に影響を与えている要因は何かを少し考えてみましょう。
カイ二乗の表を再度覗いてみます。

大阪の巨人ファンは17.83、阪神ファンは29.44とひと際大きな値を示しています。
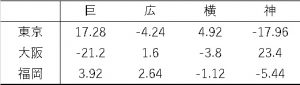
上の図は実現値-期待値の偏差です。これを見ると、大阪の巨人はマイナスで阪神ファンはプラスです。
以上のことを総合すると、
「q=0.42と多少の相関がみられる。大阪の巨人ファンと阪神ファンのカイ二乗が大きいことが寄与しているように見られる。このカイ二乗は巨人ファンにおいてはマイナス、阪神ファンはプラスである。
ゆえに大阪では巨人がファンが少なく、阪神ファンが多いために相関関係が生まれていると言える」
となります。
相関性を表す指標はクラメールの関連指数に限らず、それだけではなぜそのような相関性になっているかは分かりません。
扱う際は「なぜその数値になったのか」生データの分析を忘れないようくれぐれもご注意ください。



コメント