統計といえば、標準偏差σです。
標準偏差とは、平均からの個々の値の偏差を標準化した数値であり、バラツキを表現する代表的な数値です。
しかしながら、この標準偏差を皆さん使うことは出来ていますか?
ただそういうものがあると知っているだけでは、仕事に役立てることは出来ません。
今回は標準偏差を使う場面について考えてみます。
平均値が同じ集団の違いが分かる
店舗Aと店舗Bの売り上げを考えてみます。
1年間を通してみて売り上げの平均はA,Bともに1500万円/月とします。
平均だけを見ると両店舗とも同じ売り上げ能力を持っているように見えます。
しかしここで分析の手を止めてはいけません。
平均を見たら次に必ず標準偏差を見る習慣をつけましょう。
標準偏差を見ると
店舗A:500万円/月
店舗B:50万円/月
でした。この数値が何を意味するかお判りでしょうか。
それは店舗Aの方が売り上げに関してバラツキが大きい。
つまり
店舗AはBほど安定した売り上げを確保出来ていないということになります。
安定した売り上げが確保出来ていないのに、平均売り上げが並んでいるということはどういうことでしょうか。
これをグラフで表現すると以下のようになります。
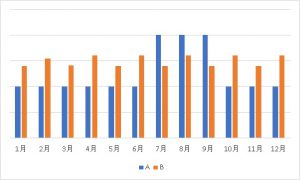
このようにバラツキが大きいということは、一時的に大きく売り上げている時期があれば、反対に売り上げが低い時期もあるということです。
標準偏差が大きくなるにしたがって、平均値は実態からかけ離れた数値ということになっていきます。

この二つの集団は平均値は同じ値(3000)ですが、左のグラフにおいて平均値3000が集団の代表値とは言い難いものとなっています。
グラフを都度描くのは大変ですが、標準偏差ならエクセルにて簡単に算出出来ます。
平均値を算出した際は必ず標準偏差も算出する習慣をつけましょう。
値のばらつく範囲を予測できる
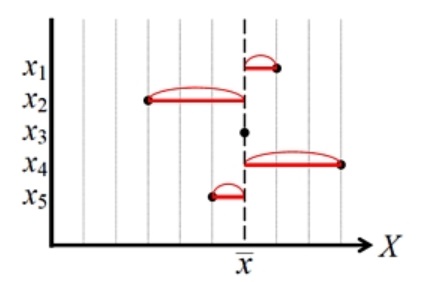
平均値と標準偏差が算出された場合、対象の集団が正規分布しているときは
平均値±nσ
の範囲にどれだけのデータが収まるのかを予測することが出来ます。
先程の売り上げに関しても、店舗Aの場合は1500±1.96×500≒600~2400万円の間を95%のデータが収まる計算になります。
つまり年間の売り上げ推移のデータから
「最低でも1000万円か」
と安心するのではなく、
「600万円になる月が出てもおかしくない」
と警戒する必要があるのです。
資金繰りに支障が出るレベルであるならば、早急に対策が必要になるわけです。
対して店舗Bの場合は、同様の計算をすると1500±1.96×50万円=1400~1600万円であり、それほど問題にならないレベルだと予測できます。
このように標準偏差が異なる場合、平均値が同じでもリスクが大きく変わってきます。
また標準偏差を算出すると先ほどの例のように、あらかじめ取るべきリスクを予測することが出来、実際に最悪の事態に陥ったとしても、対応を準備することが出来ます(もちろんそうならないように事前に対策を打って是正するのが最良です)。
このように、標準偏差の主な使い方としては
・平均値を算出するときに、無条件に標準偏差を算出する
・平均±nσでどのくらいの値が発生するのかを予測する
の2点がメインになると考えられます。
このような扱い方を癖付けると、自然と
「なぜこれだけバラつくのだろう」
と疑問を持った目でデータを見るようになります。
先程の店舗A,Bの例でいうと、Aは7~9月と夏に売り上げが集中しているために、バラツキが大きくなっていると推測できます。そこから夏に顧客が買うような効果が出ていることが分かり、
・夏の売り上げが無くなった場合どうするか
・夏にそもそもなぜ売り上げが上がったのか、そこから他の時期や他店舗に横展開出来ないか
といった考えが出てきます。
標準偏差はこのようにして使うことで、分析をよりよく行わせるきっかけとなります。
標準偏差が一般化されていない職場では、最初は他の人に説明するのが大変で、忌避してしまうこともあるかとも思います。
しかし、使わなければ使えるようになりません。
どんどん使って、慣れて、分析力を上げていきましょう。
当サイトを閲覧下さる皆さまは、日々より良い仕事が出来るようになりたいと思われているビジネスパーソンがメインだと思います。 でも「時間が無い」、「セミナー行くの面倒くさい」といった理由で中々学べていない方も多いと思います。 このビジネス動画学習サービスでは、いつでも、どこでもスマホ一つでビジネススキルを隙間時間で学ぶことが出来ます。 youtube紹介はこちら


コメント