仮説検定(以下検定)を実施することで、母集団に差が有るのかどうか評価することが出来ます。
統計の入門書にも、推定と並び必ず記載される程重要な手法です。
しかし、その検定がどれだけ信頼出来るのか、実は入門書の内容だけでは不十分だったりします。
今回は検定の確からしさを保証する、検出力について解説します。
検定の問題点
分布の重なり具合
検定のフローに関しては以下の記事に書いてあります。
このフローは入門書にも載っているのですが、実は抜け落ちている情報があります。
それは分布の重なり具合です。
一般的に解説されている検定の方法では、
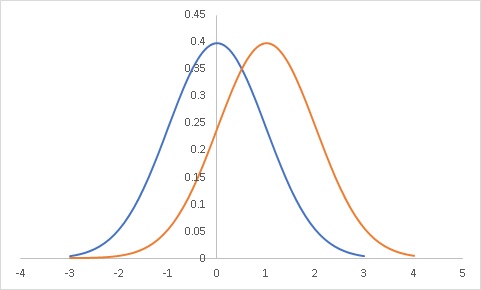
と
を区別する方法が抜け落ちています。
後述しますが、この分布の重なり具合は効果量という数字で表現されます。
サンプリングする前に、推測で設定したり、検定後に再計算したりするのです。
サンプルサイズの設定
サンプルサイズは検定結果を大きく左右します。
通常サンプルサイズは大きければ大きいほど良いと考えがちですが、実は違います。
検定においては大きすぎても、小さすぎてもダメなのです。
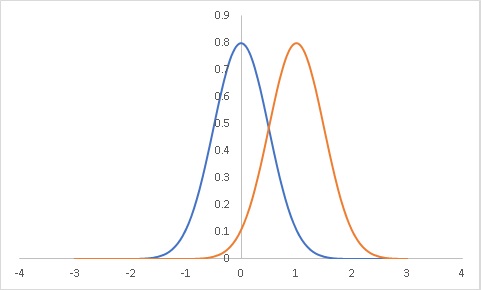
ケース1:サンプルサイズが小さすぎる場合
母集団A:平均値0 標準偏差1 サンプルサイズ2
母集団B:平均値1 標準偏差1 サンプルサイズ2
のように標準偏差1つ分という十分に平均値が離れている場合、おそらく有意差があると思われますが、サンプルサイズが小さすぎる場合、有意差なしとなってしまう可能性があります。

平均値の分布は中心極限定理により、N(μ,σ2/n)となります。サンプルサイズが小さいと”ばらつき”が大きくなってしまうのです。
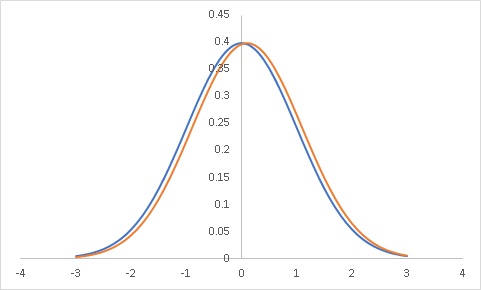
ケース2
母集団A:平均値0 標準偏差1 サンプルサイズ10000
母集団B:平均値0.1 標準偏差1 サンプルサイズ10000
と明らかに有意差が無さそうな分布でも、サンプルサイズが大きすぎると有意差ありとなってしまう可能性があります。

平均値の分布は中心極限定理により、N(μ,σ2/n)となります。サンプルサイズが大きいと”ばらつき”が小さくなってしまうのです。

この事から分布の重なり具合(効果量)に合った適切なサンプルサイズを設定する必要があります。
検出力とは
帰無仮説を正しく棄却する確率
検出力は帰無仮説H0を正しく棄却する確率の事を言います。
第一種の過誤の確率αと第二種の過誤の確率βを表で表すと以下のようになります。

検出力は1-βなのです。
αとβを分布上で表すと、
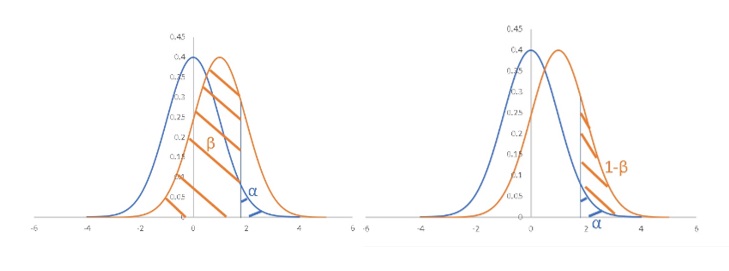
こんな感じです。
この分布を見て頂けるとお判りいただけると思いますが、分布同士の距離や”ばらつき”でαは変動しませんが、1-βは変動します。
検出力の最適値は?
検出力は0.8が最適値とされています。
この値より小さい場合は、過剰に帰無仮説が採択されやすく、大きい場合は過剰に対立仮説が採択されやすいです。
効果量Δとサンプルサイズ
先述したように検出力は、分布の重なり具合で変化します。
この分布の重なり具合は効果量Δとサンプルサイズで決定します。
効果量Δは以下の式で表現されます。
母平均の検定時
$$Δ=\frac{μ-μ_0}{σ_0}$$
母分散の検定時
$$Δ=\frac{σ}{σ_0}$$
この効果量Δですが、検定の前は自分で決める必要があります(検定後はサンプルからの値から計算出来ますが)。
こればかりは、それまでの実績で平均や標準偏差を当てはめて算出するしかありません。
また、サンプルサイズも重要です。先述したようにサンプルサイズが大きすぎても小さすぎても求めている結果が得られなくなります。
通常は検出力を0.8として、効果量Δを決定することで適切なサンプルサイズを決定します。
また検定完了後は、検定に用いた効果量やサンプルサイズを用いて検出力を算出出来ますので、結果としてどの程度の検出力で検定出来たか確認します。
詳細は以下の記事を参照ください
まとめ
検出力を押さえることで、適切なサンプルサイズでの検定が可能になります。
しかしこの検出力について言及している書籍というのは、あまり見かけません。
書籍できちんと勉強したいという方もいると思いますので、最後に本を紹介します。
 | 新品価格 |
こちらの本に、検出力、効果量からのサンプルサイズの決定方法が網羅的に記載されています。
結構難しい内容なのですが、基本的に同じ構成を繰り返す形で様々なシチュエーションを紹介してくれますので、段々と読み慣れてきます。
ぜひご一読ください。
統計リテラシーが向上するはずです。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント