2つ以上の事物の一方が変化すれば、もう一方も連動して変化する関係を相関関係と呼びます。
・売上や利益が何と相関しているのか。
・特定のスペックが、どのような条件と相関しているのか
ビジネスを行う上で、相関関係というものは最も重要な関心事です。
統計学では、このような相関関係の度合いを一つの代表値で表現しています。
今回はその代表値、相関係数の考え方、公式そしてエクセルでの関数について紹介いたします。
youtubeでも取り扱っています。ぜひご覧ください。
相関関係とは
相関関係を考えてみよう!
相関関係というものを、今一度考えてみましょう。
「あるxとyに相関関係があるか」
これを考える場合(例えば、英語の点数(x)と数学の点数(y)や、塗料の粒子径(x)と光沢度(y)など)
まずは偏差(各値-平均値)、つまり平均点をどの程度上回っているもしくは下回っているかを考えます。
$$x-x_m$$
$$y-y_m$$
xm及びymはそれぞれの平均値です。
そしてこの偏差の積を考えます。
(1)x-xm > 0, y-ym> 0のとき(x-xm)(y-ym) > 0(つまりプラス)
(2)x-xm < 0, y-ym> 0のとき(x-xm)(y-ym) < 0(つまりマイナス)
(3)x-xm < 0, y-ym< 0のとき(x-xm)(y-ym) > 0(つまりプラス)
(4)x-xm > 0, y-ym< 0のとき(x-xm)(y-ym) < 0(つまりマイナス)
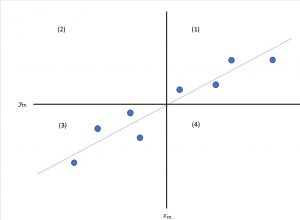
となり、これを図示すると以下のような4事象の関係性になります。

(1)xが大きい時、yも大きい
(2)xが小さい時、xは大きい
(3)xが小さい時、yも小さい
(4)xが大きい時、yは小さい
この時、値が(1)と(3)に多く入る場合、xが大きくなるとyが大きくなり、xが小さくなるとyが小さくなる。つまり相関関係があると言えます。
また逆に(2)と(4)に多く値が入る場合、xが小さくなるとyが大きくなり、xが大きくなるとyが小さいくなる。これも関係性が見えるため相関関係があると言えます。
相関関係がない場合というのは、(1)と(2)、(1)と(4)のような先ほどの関係以外の状態を言います。
先ほどの図の4事象に入った各偏差に近似的な直線を引いた場合に、斜めの線が引ける場合が相関関係があるという状態です。
この辺りは、別の動画で個別に解説しています。
相関係数 r
相関係数の公式
そしてこの相関関係の強さを表す数値が相関係数です。
公式は以下になります。
$$r=\frac{\frac{1}{N}\sum(x-x_m)(y-y_m)}{\sqrt{\frac{1}{N}\sum(x-x_m)^2}\sqrt{\frac{1}{N}\sum(y-y_m)^2}}$$
この相関係数rは-1~+1の値を取り、
・+1に近づくとyはxに比例(つまり(1)と(3)の相関関係性であり、正の相関と言います)
・-1に近づくとyはxに反比例(つまり(2)と(4)の相関関係性であり、負の相関と言います)
を示します。そして
・0に近いと相関関係はない(無相関といいます)
ということになります。
また、rは+1もしくは-1に近づくほど相関性が強いということになります。
相関係数を使えば、相関性の強さを測ることが出来ますし、比較をすることもできます。
しかしながら注意点もあります。
どこからが相関性があると言えるのかは決まっていない。
相関関係を数値で表すことが出来る相関係数ですが、どの値から相関関係があるのかは実は分かりません。
0.5からかもしれないですし、0.9は必要かもしれません。
これは評価する対象によって異なってきます。
経験的には0.5を超えたら多少の相関関係はあると見なせると私は考えますが、より精度を高めるならば、無相関の検定を行うのが良いです。
$$t_0=\frac{|r|\sqrt{n-2}}{\sqrt{1-r^2}}$$
このt0はt分布に従うので、この数値を求めたうえで「帰無仮説:相関はない」を立てたうえでt検定を行えば、相関性の有無を検定出来ます。
直線的な相関関係しか評価出来ない
先ほどまでの図を見て頂いたように、相関係数は偏差の直線的な関係を前提とした指標になります。
つまり、一次式的な関係でないと正しく評価出来ません。
二次式的、三次式的といった、グラフ化した場合明らかに相関がありそうなものでも、相関係数はその相関性を測ることは出来ないのです。
過信してエクセルでとりあえず相関係数を算出していたら、足元をすくわれる可能性大です。
エクセルによる相関性の分析
エクセルで相関性を分析する際は、
・グラフの散布図で2つの変数をプロットして、相関関係を図示する
・相関係数の関数 =correl()で相関係数を算出する。
この2点を実施し、相関関係を確認します。
相関係数だけでは、先述したように実際には二次的、三次的関係の相関を見逃す可能性があります。
一方散布図だけでは、見た目で相関関係があるように見えても実際には大した相関係数ではない可能性があります。
グラフと指標の両者を確認して、判定しましょう。
これは、相関関係に限らず統計での分析全般に言えることです。
まとめ
相関関係を測るために、相関係数は非常に役立つツールではありますが、すべての関係性に適用できるものではありません。
その点を気を付けるようにして使用していきましょう。
おススメ記事




コメント