仮説検定を使うことで、ある程度の確率で有意差の検討を行うことが出来ます。
しかしながら、ある程度の確率ということは、間違える可能性もあるということです。
今回は、その誤りについて解説していきます。
誤りには主に2種類あります。
・第一種の過誤:本当は差がないのに、差があると間違えてしまうこと
・第二種の過誤:本当は差があるのに、差がないと間違えてしまうこと
第一種と第二種の過誤とは

第一種の過誤
本当は差がないのに、差があると間違えてしまうことを第一種の過誤と言います。
これは
『間違えて対立仮説を採択する』
と言い換えることも出来ます。
第一種の過誤をしてしまう可能性は、有意水準αと同じです。
有意水準α=5%より外れるということは、
差がない場合、5%の確率で発生することが起こった
ということなのです。
それを差があるということの区切り目にしようと、評価者が決めているだけで、当然100回のうち5回しか起きない出来事が、偶々起こったということもあり得るのです。
第二種の過誤
本当は差があるのに、「差がない」と間違えてしまうことを第二種の過誤と言います。
これは
『間違って帰無仮説を採択する』
と言い換えることが出来ます。
第二種の過誤はβと言われ、帰無仮説の分布と対立仮説の分布の間で以下のような関係があります。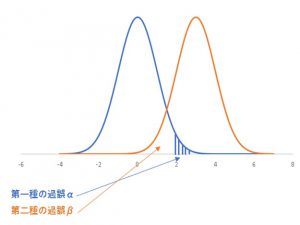
つまり差が無い青の分布のα=5%より内側に被っている差がある橙の分布の部位が、第2種の過誤の発生確率になります。
第一種の過誤はαと一致していましたが、βは分布同士の被り具合によって変わってきます。
当然、分布同士の差が大きいとβは小さくなりますし、分布同士が近いとβは大きくなるという訳です。
この辺りは検出力1-βの概念を理解する上で非常に大切なので、よくよく押さえておきましょう。
αとβの関係
先ほどの図を見て頂けると分かるように、αが小さくするとβが大きくなり、βを小さくするとαが大きくなります。
これは、第一種の過誤と第二種の過誤、両方の確率を同時に小さくすることは出来ない、つまりトレードオフの関係にあることを意味します。
このために、検定という作業は常に間違った判断をしてしまう可能性を孕んでいます。
出来るだけ検定による判断ミスを回避するには、グラフによる比較も実施し総合的に判断しなければなりません。
第一種と第二種 いずれの過誤が重要か

第一種の過誤の方が重要です。
トレードオフの関係にある以上、第一種の過誤と第二種の過誤いずれの可能性を優先的に小さくするべきでしょうか。
この議論では、以下のような例え話で説明されます。
ある裁判において、容疑者に対しての判決を考える場合、帰無仮説は
「容疑者は真犯人ではない(容疑者=無実の人)」
となります。
母集団は無実の人の集団だからです。
この場合
第一種の過誤:容疑者は冤罪で犯人にされる(容疑者≠無実の人)
第二種の過誤:容疑者は真犯人なのに、逃がしてしまう
どちらが深刻かと言えば、第一種の過誤です。第二種を優先した場合、灰色は黒とされてしまう可能性が高くなるのです。
つまり
毛利小五郎は罪深いのです。

このように、第一種の過誤はその他大勢の人間に対して、被害を与える可能性が高く危険なため、基本的には第一種の過誤を小さくして、その中で出来るだけ第二種の過誤を小さくする手法を選ぶというのが、セオリーです。
第一種の過誤とされているのも、そういった事情があるからです。
過誤は分かりづらい どっちがどっち?
理屈は分かるのですが、第一種と第二種の過誤は
「どっちがどっちだったっけ」
といつも混同してしまいがちです。
皆同じ悩みを持っているようで、このようなゴロ合わせが一般的に言われています。
あわてんぼのα(第一種)
ぼんやりもののβ(第二種)
「何があわてんぼなんだ?」と突っ込んだ記憶があります。
分かりやすいのかどうか、釈然としない人も多いと思います。
先程の冤罪の例を思い出してほしいのですが、基本的に探偵ものの迷探偵(毛利小五郎とか)は証拠が不十分なのに慌てて犯人を仕立て上げてしまいます。
この慌ててというのは、
「証拠が足りない」
という状況の事を指します。
これは検出力という検定において重要な考えにも通じるのですが、とりあえず
「証拠(サンプルサイズ)が不十分な状態で、有意差ありにしたら一番ヤバい」
と毛利小五郎の姿を思い描いたら、少しは覚えられるかもしれません。
まとめ
仮説検定は確かに有効なツールですが、以上のような誤りを犯す可能性が常にあります。
しかもどっちの過誤が重要か混同してしまいがちでもあります。
こういった状況を避けるためには、過誤というものの認識を正しくする事と、検定だけで判断せず、グラフ等複数の手法を併用し総合的に判断する事が重要になります。
検定に限らず、統計では一つの手法に頼り切ると思わぬミステイクをしてしまう可能性もありますので、そのあたり重々注意して分析していきましょう。
あとがき
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう




コメント