私たちはよくデータを採取すると、算術平均を導いて比較をしたりします。
この平均値、外れ値が存在していると引きずられてしまうという欠点がありますが、そんな性質を補って余りある性質を持っています。
この平均値に関連する性質として、
大数の法則
中心極限定理
の2つが挙げられます。
実は、これらの性質のおかげで、
・サンプルサイズを大きくすると精度が上がる
・z検定やt検定などの活用で、元データの分布を考慮しなくても良くなる
などの恩恵にあずかれるのです。
今回は、この2つの性質について解説いたします。
この本を参考にしていますので、興味のある方は手に取ってみて下さい。
動画でも紹介しています。
統計学の問題点 正規分布前提
正規分布を前提とする手法で良いのか?
統計学の入門書に記載されている手法は、z検定、t検定、平均値の推定などが挙げられますが、どれも正規分布であることを前提としたものばかりです。
実際に学び始めた際は、
「正規分布じゃなかったら、どないするんじゃーい」
と、一人心の中でツッコミを入れたものです。
基本的にはQ-Qプロットやシャピロ-ウィルク検定で判断する事は出来ますし、
もし正規分布でなかった場合、ノンパラメトリック分析を活用すれば良いのですが、
統計を学び始めたときは、これらの手法を活用するのは多少ハードルが高いです。
出来ればこういう煩わしいものは、避けてもっとお手軽に検定とか使いたいですよね?
ですが、ご安心。
t検定や平均値の推定などは、元分布が正規分布じゃなくても使う事が出来ます。
更にサンプルサイズが大きくなるほど、その予測精度は向上していきます。
なぜなら、サンプルから構築された分布には中心極限定理と大数の法則が成り立つからです。
大数の法則とは?
まず、大数の法則から解説します。
まず、こちらのシチュエーションで考えてみて欲しいのですが、
サンプルサイズN=10 サンプル数 5
サンプルサイズN=30 サンプル数 5
この2つの場合で、それぞれ平均値を算出した場合、どちらの方が真の平均値をより良く予測出来そうですか?
おそらく、皆さん後者のN=30の方を選ぶと思います。
それは、皆さんが経験的に沢山のデータから平均値を出した方が正確であるという事を、経験的に知っているからです。
大数の法則とは、測定を無限回行えば期待値に収束していく法則を指します。
言い換えれば、何回もやると精度増すぜって事です。
ここで、元の分布と標本分布にも注目してみましょう。
元の分布を
元分布:N(μ,σ^2)
とした場合、そこからサンプルサイズnで平均値を算出すると、その平均値は
標本分布:N(μ,σ^2/n)
と、真の値を予測しやすくなります。

このように、大数の法則のおかげで一回における実験のサンプルサイズを大量にすることで、精度の高いデータを得る事が出来るわけです。
例えば納期が迫っている場合に、実験が一回しか出来ないってなった場合は、その一回の実験におけるサンプルサイズを大きくしておけば、データの精度は向上するという訳です。
時間が無い時には、ぜひこれを念頭に入れて、データ採取をしましょう。
中心極限定理とは?
中心極限定理の解説をいたします。
こちらの性質の方が重要だと思います。
この定理は、平均値が描く標本分布の形状は、元の分布に関係なく正規分布を描くというものです。
スゴくないですか?
元分布に関係なく、正規分布にもっていけるんですよ?
そりゃ、様々な統計の手法が正規分布前提になるってもんですよ。
平均値が正規分布を形成するので、
t検定
平均値の推定
xbar-R管理図
この辺りは、元の分布の形状を気にしなくても良いわけです。
この中心極限定理も、サンプルサイズを大きくすればOKです。
それでは、どのくらいサンプルサイズが必要になるのでしょうか?
どのくらいのサンプルサイズが目安?
大数の定理と中心極限定理のおかげで、サンプルサイズさえ十分に大きければ基本的に正規分布を前提とした手法を扱うことが出来そうです。
ここで気になるのは、どの程度のサンプルサイズが必要なのかということだと思います。
まず大数の定理に関してですが、おおよそN≧30くらいです。
以前の記事で、サンプルサイズによる統計量の精度についての記事を上げていますので、詳細はこちらを参照ください。
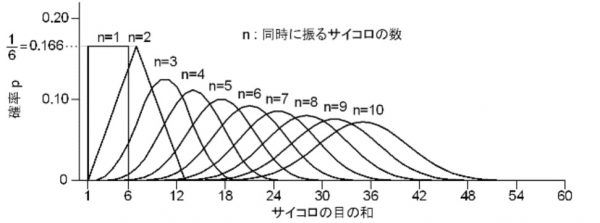
そして中心極限定理ですが、大体N=5以上になると元が一様分布だろうが、二項分布だろうが、非対称な分布であろうが大抵の標本分布は正規分布と区別できなくなります。
検定の場合などは、サンプルサイズが大きすぎても検出力が高くなりすぎて、第一種の過誤を起こしやすくなります。
ですがサンプルサイズ5程度なら、その縛りからも、解放されることになると思います。
まとめ
大数の定理と中心極限定理のおかげで、迷いなく正規分布前提の手法を扱うことが出来ます。
質的データの場合はこうも行きませんが、量的データの場合は、とりあえずサンプルサイズ5以上を揃えた上で統計的手法を活用してみて下さい。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント
“元分布:N(μ,σ^2)とした場合、そこからサンプルサイズnで平均値を算出すると、その平均値は標本分布:N(μ,σ^2/n)”
というのは、なぜでしょうか。