以前正規分布を用いた、平均値の区間推定を紹介しました。
しかしながらこの方法は少ないサンプルサイズ(小標本)では不適切とされています。
とは言っても少ないサンプルサイズしか採取できないシチュエーションの方が多いハズ。
そんな中で、なんとか真の平均値の範囲を押さえたい。
そのようなときに代用出来るのがt分布を利用した平均値の推定です。
n数が少ない場合に正規分布の代わりにt分布を使用するというのは、検定の場合と同じです。
今回はt分布を利用した、小標本での平均値の区間推定を紹介いたします。
今回の内容は、以下の本でも紹介しています。
動画でも解説しています。
t分布を使った区間推定

t分布って何だっけ?
t分布とは、自由度(サンプルサイズ-1)によって形状を変える性質を持った分布であり、自由度が極めて大きくなると正規分布に近づきます。
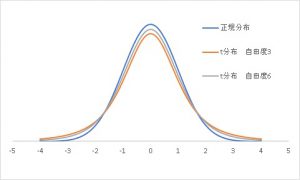
サンプルサイズが小さい時には、裾野が広くなるため
・サンプルが少ないと、精度が悪くなる
という現象に対応できる点がミソです。
正規分布の場合のように、t分布にもt分布表があります。
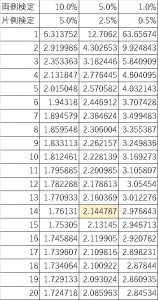
黄色部分は両側推定95%(もしくは片側推定97.5%)で自由度n-1=14の時のt値になります。
t分布による推定
区間推定は以下のように進めます。
1,統計量(平均値,分散)を求める
2,統計量の標準化を行う
3,95%信頼区間を求める
4,標準化した統計量を式変形して元の統計量の区間を導く
t分布による推定では、正規分布による推定と違いt値という統計量を使います。
t値は以下のように算出します。
$$t=\frac{\overline{x}-μ}{s/\sqrt{n}}$$
ただしμは母集団の平均値です。
この式ですが、一見するとz値と同じに見えます。
違いは、正規分布は母集団の標準偏差σを使うのに対して、t値では標本の不偏標準偏差sを使用する点です。
t分布による推定は、母分散が未知という前提で行われるために、母分散であるσではなく、サンプルからの予測値である不偏標準偏差sを使用しているのです。
ですが実際には正規分布の母数は分からないので、結局sを使用することになっており、まったく同じ式になってしまっています。
それでは、実際にt分布による推定をやってみましょう。
例として以下のデータを使用します。

まず、平均値と標準偏差を求めます。
$$\overline{x}=4.3$$
$$s=3.0$$
になります。
次にt値を算出します。
$$t=\frac{\overline{x}-μ}{\frac{σ}{\sqrt{n}}}=\frac{4.3-μ}{\frac{3.0}{\sqrt{10}}}$$
次にt値の95%信頼区間をもとめます。
本来はt分布表で確認するのですが、面倒くさいのでエクセル関数を使いましょう。
今回は両側の範囲を決めるので、T.INV.2T関数を使用します。
=T.INV.2T(確率,自由度)
今回は確率に0.05、自由度に7(=8-1)を入力します。答えとしては2.365が返ってきます。
なので、これらをまとめると
$$-2.365 < \frac{4.3-μ}{\frac{3.0}{\sqrt{10}}} < 2.365$$
となります。後は “< μ <“の形になるように変形します。
$$4.3-2.365×\frac{3}{\sqrt{10}} < μ < 4.3+2.365×\frac{3}{\sqrt{10}}$$
$$1.792 < μ < 6.808$$
これでおしまいです。
正規分布 vs t分布の区間推定
ここで以前同じデータを使って正規分布で区間推定した結果と、今回の結果を比べてみましょう。
正規分布による推定 2.4 < μ < 6.2
t分布による推定 1.8 < μ < 6.8
t分布による推定の結果は、正規分布より広くなっています。
これは、サンプルサイズが8という小標本では正規分布では対応しきれていない事を如実に示しています。
このサンプルサイズが大きくなっていけば、正規分布による推定の結果に近づいていきます。
推定の豆知識ポイント
t分布と正規分布の境目は?
t分布はn数が増えるほどに正規分布に近づいていきます。
ということはt分布表の95%信頼区間が1.96に限りなく近づくn数を探っていけば、正規分布での推定(または検定)で必要なサンプルサイズが分かるはずです。
ということでエクセルで探ってみました。
=T.INV.2T(確率,自由度)
この関数でt分布表が作れるので、この式が1.96になる自由度を探りました。
とは言え完全に交わることはなく、限りなく1.96に近づく近似値しか出ないと思いましたので1.961になったn数を確認しています。
結果としては、n=2280で1.961に一致しました。
ただグラフにすると、n=500でほぼサチっている(飽和している)ようなので500もあれば十分という感じもします。
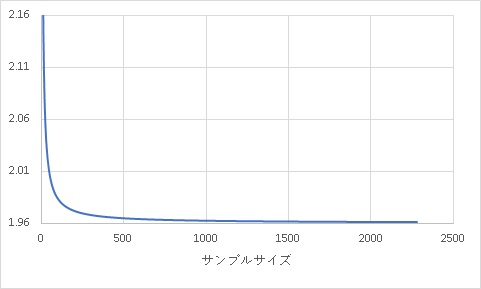
思った以上に大きなサンプルサイズになっています。
母分散既知の推定を行う時には、500以上のサンプルサイズを準備しましょう。
まとめ
t分布を使えば、少ないサンプルサイズでもそれに応じた推定が可能になります。
またサンプルサイズが増えれば正規分布による検定と一致していくので、結果から言えば正規分布による検定は念頭に置かず、t分布の使用だけ考えればいいように思います。
正規分布とt分布どっちを使おうか悩む時間があるなら、他の仕事を進めた方が有意義です。
平均値の推定、検定を実施する際は迷わずt分布を使いましょう!
あとがき
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント