統計を学習する上で、そりゃもう様々な分布が出てきます。
矩形分布、ポアソン分布、正規分布
その中で、中々何のために存在するのか初見ではよく分からない分布
それが、カイ二乗分布です。
私自身、初見のときは、よく分からなかったんですよ。
ていうのも、あまり仕事で使う機会に恵まれなかったですから。
とはいえ、カイ二乗分布はばらつきの検定、推定、そして標準偏差のサンプルサイズにと結構いろんなところに顔を出す分布ですので、押さえておくべき分布ではあるのです。
という事で、今回はカイ二乗分布の解説と、その実用例として、ばらつきの検定を解説いたします。
カイ二乗分布とは何?

ばらつきに関しての分布です
そもそもカイ二乗分布って言葉では、何に関する分布なのか分かりません。
これが、理解を妨げている原因ですね。
ズバリ、カイ二乗分布は分散、つまりバラツキに関しての標本分布のことを言います。
バラツキの比較検定を行う際に使用する、F検定のF分布もカイ二乗分布が元になっています。
母分散と不偏分散の比に自由度を掛けた数値
$$x^2=\frac{(n-1)s^2}{σ^2}$$
(ただしσ2は母分散、s2は不偏分散)をカイ二乗値と呼びます。
母分散は常に一定の数値ですが、不偏分散はサンプリングの度に異なるためにx2は分布を形成するのです。
カイ二乗分布は自由度によってその形状は異なります。
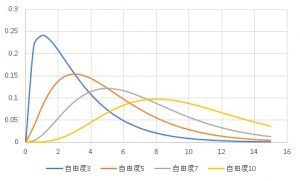
カイ二乗分布は分子と分母ともに標準偏差を2乗した分散値なので、正の値しかとりません。
なのでカイ二乗分布も正の値しかとりません。
また不偏分散の期待値(平均値)は、母分散です。(不偏分散は母分散を知るための算出値です)
なので、x^2の期待値(平均値)はn-1と自由度と同じ値になります。
母分散と不偏分散が等しいと
$$x^2=\frac{(n-1)s^2}{σ^2}=\frac{(n-1)×1}{1}=n-1$$
となるからです。
そして、自由度と平均値(つまり最頻値)が等しいので、自由度が大きくなるにつれて分布の山が、大きな値にずれていきます。
そして、平均値の周りに均等にばらつく正規分布に似た形状になっていきます。
カイ二乗分布は何に使えるのか?
ここで、カイ二乗分布というものはどういったものか、イメージは掴めてきたかもしれません。
ですが、肝心なことは
「何に使えるのか?」
の一点だと思います。
専門家ではない一般的なサラリーマンとしては、学術的な意味よりも道具としての有用性に興味が向くはずです。
カイ二乗分布の使い道としては、
・分散の推定
・母分散の分散が特定の分散値に等しいかの検定
・2つの分類基準が独立であるかの検定
と便利そうなものが並んでいます。
とりあえず、今回はその一例として、分散の検定について紹介したいと思います。
カイ二乗分布で分散の検定をしよう

検定の考え方の復習をしよう
カイ二乗分布を利用する事で、1群のばらつきの検定を実施する事が出来ます。
1群の検定とは、比較対象となる分布とサンプリングしたデータが一致するのかを検証する手法です。
これを使う事で、数字を単純に比較するだけでは分からなかった有意差を一定の確率の元言及することが出来ます。
順序としては、
①帰無仮説の設定
②対立仮説の設定
③有意水準の設定
④検定統計量の算出
⑤検定統計量と分布の有意水準に合致する値を比較する
となっています。
具体的な手順は以下の記事に記載していますので、参照してください。
帰無仮説の設定
まずは、帰無仮説を設定します。
$$s^2=σ^2$$
ただしs2は不偏分散、σ2は設定した特定の分散です。
不偏分散が母分散と等しいという風に、帰無仮説を設定するのです。
例えばある生産ラインの分散値は、これまでの実績から3で管理してきました。
しかしながら、今本当に3なのかと問題になった場合、この検定を実施するとします。
その場合、
s2:サンプリングして得られた不偏分散
σ2:これまでの分散値 3
故に帰無仮説は
H0:s2=3
といった内容になります。
対立検定ごとの棄却手続き
検定では、帰無仮説を棄却した際に採択する対立仮説というものを立てます。
対立仮説s2 > σ2の場合:x2 > x2(α) 上側検定 想定より実測したバラツキが大きい
対立仮説s2 < σ2の場合:x2 < x2(α) 下側検定 想定より実測したバラツキが小さい
対立仮説s2≠ σ2の場合:x2 < x2(α/2) or x2> x2(α/2)両側検定 想定したバラツキではない
有意水準の決定
ここでは有意水準α=5%とするのが一般的です。この数値はほかの検定と変わりありません。
また両側検定の場合は、2.5%と有意水準の1/2にするという手続きも同様です。
x^2を算出する
t検定においてtを算出したように、この検定ではx^2を算出します。
$$x^2=\frac{(n-1)s^2}{σ^2}$$
n-1は自由度です。例えばサンプルサイズが20の場合、自由度は
$$20-1=19$$
となります。
カイ二乗分布表の数値と比較する
標準正規分布に標準正規分布表、t分布にt分布表があるように、カイ二乗分布にも分布表があります。
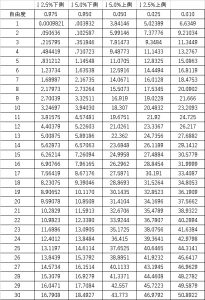
自由度と有意水準の交点の数値が、有意水準の境界になるx^2(α)値になります。
z検定やt検定と異なるのは、カイ二乗分布は非対称の分布であるという事です。
つまり、同じ有意水準5%でも、上側を見るか、下側を見るかでカイ二乗値の絶対値が変わってきます。
上側検定で有意水準5%の場合、0.05の行の自由度19で
$$x^2(α)=30.14$$
になります。
一方下側検定で有意水準5%の場合、0.95の行の自由度19で
$$x^2(α)=10.12$$
になります。
ね?数字の絶対値からして、全然違う値になったでしょ?
上側、下側、両側検定の場合に見る有意水準の場所ですが、今回のような有意水準α=5%の場合
下側検定:0.95(100-95%=5%)
上側検定:0.05(そのままです)
両側検定 下側0.975(100-97.5=2.5%) 上側0.025(そのままです)
を見ましょう。ここさえ注意すれば、通常の検定と大して変わりません。
検定
最後に算出したx2と分布表のx^2(α)を比較します。
先ほど述べましたように、対立仮説によって以下のように棄却の方法が異なりますので注意してください。
対立仮説s2 > σ2の場合:x2 > x2(α) 上側検定
対立仮説s2 < σ2の場合:x2 < x2(α) 下側検定
対立仮説s2 ≠ σ2の場合:x2 < x2(α/2)またはx2 > x2(α/2)両側検定
まとめ
カイ二乗分布は、その名前から何の分布なのか分かりづらいです。
でも、なんてことはない、ばらつきの分布なんです。
これを押さえておくことで、一群のばらつきの検定や適合性の検定とかも使えるし、F検定の基礎にもなっていたりするので、非常に大切な分布何です。
ちょっと避けたくなる気持ちを押さえて、しっかり学習していきましょう。
今すぐ、あなたが統計学を勉強すべき理由
この世には、数多くのビジネススキルがあります。
その中でも、極めて汎用性の高いスキル。
それが統計学です。なぜそう言い切れるのか?
それはビジネスというのは、結局お金のやり取りであり、必ず数字が絡んできます。
そして数字を扱うスキルこそが統計学だからです。
故に一口に統計学といっても、
営業、マーケティング、研究開発、品質管理、工程管理、生産管理.etc
これら全てで使う事が出来るのです。
現に私は前職は品質管理、現職は研究開発職なのですが、面接のときに
「品質管理時に活用した、統計の知識を研究開発にも活かせます」
とアピールして職種をうまく切り替える事が出来ました。
そして、もし始めるなら今から勉強を始めましょう。
なんなら、今すぐこのページを閉じて本格的に勉強を開始するべきです。
なぜなら、このような『スキル』は20代でもっともキャリアアップに繋がるからです。
30代ならいざ知らず、40代になると求められるのはこれまでの業務を遂行してきた経験や人脈なのです。
これが無いとある一定以上のキャリアアップは望めませんし、40代以降のハイクラスの転職先も望めません。
20代のうちは成果を結び付けるためにこのスキルが大いに役立ちますが、年を経るごとに求められる働き方が変わるのでスキルの実績への寄与が減ってしまうのです。
なので、後からやればいいやと後回しにすると機を逸してしまう可能性が高いです。
ちなみにこれから統計学を学習をするというのであれば、ラーニングピラミッドというものを意識すると効率的です。
私自身、インプットだけでなく、youtubeや職場でアウトプットしながら活用する事で統計リテラシーを日々向上させていっています。
ぜひ、アナタも当ブログやyoutubeチャンネルで統計リテラシーを上げて、どこでも通用するビジネスパーソンになりましょう





コメント