以前は検定の検出力の計算方法を紹介しました。
今回はそこからサンプルサイズの計算方法を紹介します。
検出力を元にしてサンプルサイズを設定することで、高い検出力での検定を行う事が出来ます。
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
サンプルサイズの計算
最も簡単なサンプルサイズの算出は?
前回紹介した式
$$1-β=Pr(z≦-Z_{α/2}-\sqrt{n}Δ)+Pr(z≧Z_{α/2}-\sqrt{n}Δ)$$
ただし
$$Δ=\frac{μ_1-μ_0}{σ}$$
において1つ目の式の右辺第一項は、√nΔが非常に小さい時以外ほぼ無視できます。
よって1つ目の式は
$$1-β≒Pr(z≧Z_{α/2}-\sqrt{n}Δ)$$
と見なすことが出来ます。この式は
$$Z_{1-β}≒Z_{α/2}-\sqrt{n}Δ$$
のように解けます。これを変形すると
$$n≒(\frac{Z_{α/2}-Z_{1-β}}{Δ})=(\frac{Z_{α/2}+Z_{β}}{Δ})$$
となり、これがサンプルサイズnの算出式になります。
これはz検定つまり、サンプルサイズが膨大(100以上)な場合にのみ適用できる算出式です。
t検定の場合のサンプルサイズは?
どちらかといえば、皆さんt検定におけるサンプルサイズの方が気になるのではないでしょうか?
だってt検定の方が頻繁に使うでしょうから。
ということで、
t検定でのサンプルサイズの導出式ですが・・・
計算は割愛させていただきます。
というのも、当サイトで扱うには計算方法が難儀すぎるのです。
とりあえず、算出式だけ紹介させていただきます。
$$n≒(\frac{Z_{α/2}+Z_{β}}{Δ})+\frac{Z^2_{α/2}}{2}$$
z検定の時よりサンプルサイズが若干大きくなります。
t検定はz検定が小サンプルサイズに対応出来ないために作られているので、検出力を担保するためにサンプルサイズが増加する事は当然であると言えます。
たとえば有意水準αが5%の場合
$$\frac{1.96^2}{2}=1.92$$
と+2ほど大きくなります。
実際の使用について
サンプルサイズですが、式から
有意水準α:5%(0.05)
検出力:80%(0.8)
とセオリーどうりに決めた場合、結局Δによって決定します。
Δが大きいほどサンプルサイズは小さくなり、
Δが小さいほどサンプルサイズは大きくなります。
Δが大きいということは、平均の差μ1-μ0に対してバラツキである標準偏差が小さいということです。
バラツキが小さいとμ1≠μ0の境界が明確になるためにサンプルがそれほど必要ではなくなるのです。
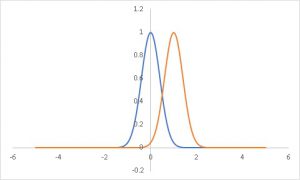
逆に標準偏差が大きい(Δが小さい)とμ1≠μ0の境界が曖昧になるので、検定の精度が落ちます。
故に多くのサンプルが必要になります。
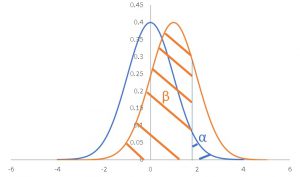
また注意点ですが、算出したサンプルサイズより無暗に大きくしたら良いというものでもありません。
検定はサンプルサイズが増えるほど帰無仮説を棄却しやすくなります。
$$σ=\sqrt{\frac{σ_0}{n}}$$
この式は元の分布の標準偏差σ0より、サンプルサイズが大きくなるほど平均値の標準偏差σが小さくなることを示しています。
分布がサンプルサイズの上昇に伴いどんどん収束していって過剰に帰無仮説を棄却しやすくなります。
そうなると第一の過誤つまりH0:帰無仮説が成り立っているのにH0を棄却してしまうという誤りをする危険性が出てきます。
故に検出力と有意水準そして設計したΔから求めたサンプルサイズ通りに検定を実施することが一番高精度ということになります。
計算が難しいという方には?
ただこの辺りの計算。
一々やっていられないというのが、本音ではないでしょうか。
実際に私もこんな計算やっている暇ないです。
仕事は常に時間との勝負。こんなことに時間をかけていられません。
なので、この辺りの検出力、サンプルサイズ設定はEZRに任せてしまいましょう。
ここにEZRでの検出力とサンプルサイズの出力方法をまとめています。
マウスと簡単な設定値入力で誰でも出来ますので、ぜひ活用してみて下さい。
まとめ
検定において検出力とサンプルサイズは非常に重要な要素です。
ですが、中々これらについて記述した文献というものは少ないのが現状です。
このサンプルサイズについて、書かれた本と言えばコチラ
今回の内容も、この本を参考に書いています。
より詳細に勉強したいという方は、ぜひ読んでみて下さい。
統計学をうまく使うために・・・
「先ほど紹介された手法を使って業務改善を行うぞ!」
と今から試そうとされているアナタ。
うまくいけば問題ありませんが、そうでない場合はコチラ
統計学の知識を持っていてもうまくいかない場合というのは、そもそも相対する問題がうまく数値化、評価が出来ない場合というのが非常に多いのです。
私もこれまでそのような場面に何度もぶち当たり、うまく解析/改善が出来なかったことがありました。
このnoteはそんな私がどのように実務で数値化をし、分析可能にしてきたかのノウハウを公開したものです。
どんな統計学の本にも載っていない、生々しい情報満載です。
また、私の知見が蓄積されたら都度更新もしていきます!!
買い切りタイプなのでお得です。
ぜひお求めくださいな。





コメント