統計を勉強していると、頻繁に目にする単語。
それが有意差です。
読んで字のごとく意味の有る差を示すもので、誤差レベル以上に差がありますという意味です。
統計では、誤差をものさしにすることでデータ同士に差が有るのかどうかを示してくれるので、この概念非常に便利なのですが、過信しすぎてはいけません。
というのも、統計的に有意差ありと判定されても本当に差があるとは限らないからです。
今回はこの有意差というものに関して、考えていきましょう。
有意差を復習しよう

有意差とは?
改めて有意差というものを復習してみましょう。
基本的に有意差検定(別称仮説検定)で活用される概念です。
有意水準をあらかじめ決めておき、その有意水準よりも低い確率で発生する統計量が得られた場合、
・有意差が無い場合に極めて低い確率で発生する事象が起こった。
↓
・有意差があると考えて方が自然。
と考える事で、判定します。
詳しくは以下の記事を参照してください。
検定における有意差
有意差を検定する際に非常に重要になるのがデータのばらつきです。
例えば平均値0と1というものがあり、この二つの間に有意差があるかどうかを考えるとします。
この平均値だけでは、判断できません。
そこでばらつき(=標準偏差)を利用します。
平均値0のデータ集団のばらつきが0.1の場合と1の場合を比較してみるとどうでしょう。
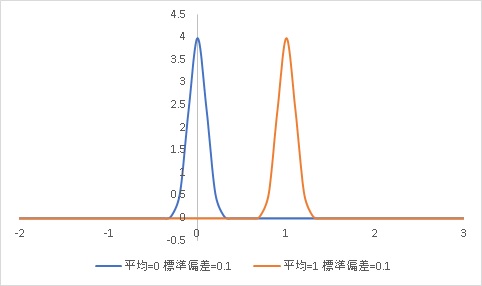
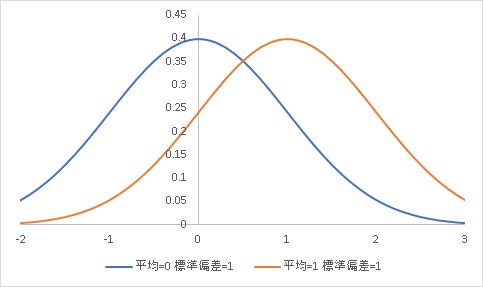
同じ平均値0と1の比較でも、標準偏差が0.1の場合は明確に分布同士に差が見えますが、標準偏差が1の時は本当に差が有るのか疑わしいことが見て取れると思います。
このように、有意差というものはばらつきや誤差を利用して差が有るかどうかを示しているのです。
ここから本題の『有意差が本当に意味の有る差なのかを考える』に入るのですが、重要なのは有意差を
何をものさしにして判断するのか?
なのです。
ここを意識してここからは読み進めてほしいのです。
統計的な有意差と専門固有な有意差

別のものをものさしにするとどうなる?
検定、ひいては統計においては有意差を”ばらつき”をものさしにして判断するのでした。
ではこの”ばらつき”というものさしはいつでも正しいのでしょうか。
いえ、決して正しいとは言えません。
次のような例で考えてみましょう。
2つの集団の身長を比較してみます。
一方は平均身長170cmで、標準偏差は0.1cmです。
もう一方は、平均身長169cmで標準偏差は0.1cmです。
分布として比較するとこうなります。
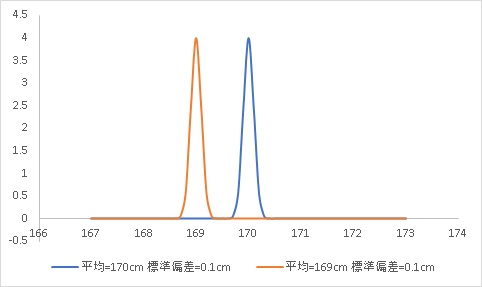
このようにグラフにしただけでも、明らかに差がありそうです。
それでは、この集団はバレーボールのチームだとしましょう。
このチームの身長差は実力差が生まれるほどの差と言えるでしょうか?
言えませんよね。
つまり、バレーのチームというものさしで見ると有意差がでる身長とは言えないのです。
このように、いつでも”ばらつき”という尺度で比較する事が正しいとは限らないのです。
専門知識というものさし
このようなバレーのチームというようなものさしというものは、数多く存在します。
・外観の傷の差
・ある境界を超えると挙動が変わるような差
このように、この世には様々な尺度が存在します。
おそらくあなたが扱っている製品にも、ばらつきとは異なる固有のものさしがあるはずです。
当然、この専門知識固有のものさしは”ばらつき”をものさしにした検定といつでも結果が一致するとは限りません。
というより、一致しない事の方が圧倒的に多いはずです。
本当は(製品固有の差から見れば)、大した差ではないが検定の結果有意差が出たから、差があると判断しようとなってしまえば、大変な間違いを犯す可能性が出てきます。
差を見るためにとりあえず検定をしよう!ってなると非常に危険なわけです。
有意差検定の活用法
さて、このように言われてしまっては、
「検定って役に立たないの?」
と言われかねません。
そんなことはありません。非常に役に立つツールであることに違いはありません。
要は使い方です。
例えば本当に差が有ると言いたい場合は、
・Xだけ差が出たときに、本当に差があると言える
という事を初めから補正してあげれば良いのです。
つまり
帰無仮説H0:μ = μ0+X
対立仮説H1:μ > μ0+X
として、検定を実施してやればOKなんです。
差が出るとされる値以上に大きくなれば、誤差的も専門的にも差があると言えるのです。
そしてこれを利用する事で、検定が苦手とする等しいという事象に対しても積極的に採択する事が可能となります。
つまりX以上差がないと差があると言えないと分かっているならば、
μ < μ0+X
μ > μ0-X
とすれば、同等であるという事が出来ます。
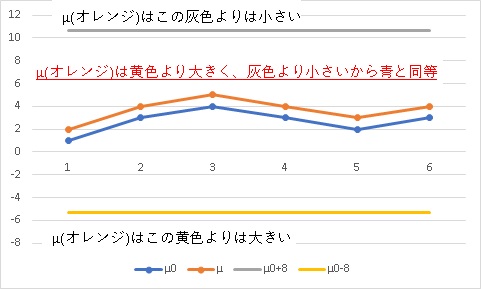
この同等であるということを積極的に採択する検定については、以下の記事を参照してください。
まとめ
検定はばらつきをものさしにして、差を比較する統計の手法です。
これは、どのような場合にも適用出来るわけではなく、扱う製品やものによって、それ固有の専門的な差によっては工夫が必要です。
この専門的な固有差は、あらかじめ検定に補正値として組み込んでおけば、有意差検定を問題なく行うことも出来ますし、工夫次第では検定が苦手とする差がないという現象も採択する事が可能となります。
検定はそのまま機械的に使っても、うまく機能しかいことが良くあります。
あなたが扱う商品、製品の特性をよく理解した上で有意差検定を行っていってください。
その他おススメ書籍はコチラ
当サイトを閲覧下さる皆さまは、日々より良い仕事が出来るようになりたいと思われているビジネスパーソンがメインだと思います。 でも「時間が無い」、「セミナー行くの面倒くさい」といった理由で中々学べていない方も多いと思います。 このビジネス動画学習サービスでは、いつでも、どこでもスマホ一つでビジネススキルを隙間時間で学ぶことが出来ます。 youtube紹介はこちら




コメント