こんにちは、熊野コミチです。
仕事で使える統計学を発信していると称しておきながら、最近は品質工学にがっつり偏っています。
というのも、2022年6月現在の私が携わっているのが、新製品の立ち上げでして統計学よりもパラメータ設計を使う機会が多いからです。
という事で今回も品質工学関連なのですが、今回はエネルギー比型SN比を紹介したいと思います。
この概念は鶴田明三氏が提唱したもので、従来のSN比のデメリットを解消したものです。
しかしながら初出が2008年頃でまだまだ文献も少なく、関連記事もあまり見かけません。
ですが、僕自身見様見真似で活用したところ、グラフイメージとも合うし、計算も簡単でとても使いやすかったので超おススメなんです。
という事で、自信は全くないですが、この手法を少しでも多くの方に使ってもらうべく今回はこのエネルギー比型SN比を解説します。
参考文献
StatWorks/V5®(品質工学編)の新機能“エネルギー比型 SN 比”を用いた設計品質の評価
考案者の書籍
品質工学でのSN比とは?
加法性のあるばらつきの指標
まずは従来の品質工学におけるSN比の説明をしましょう。
SN比は本来は電子工学などで使われている指標です。品質工学特有の概念じゃないんですよ。
これは元々創始者である田口玄一博士が、電電公社やベル研究所など信号を扱う業界にいたところから着想を得ているんでしょうね。
SN比はシグナル-ノイズ比の略称です。シグナルは欲しいもので、ノイズは欲しくないもの。
SN比=シグナル/ノイズ
つまり、SN比が大きいほど、欲しいものが多いという事を表す指標なんです。
品質工学では、このSN比をばらつきの指標として扱います。
通常の製品の測定値でいうと、シグナル(分子)が平均値でノイズ(分母)がばらつきです。
「なんで比で表すの?分母にもってきてるばらつきで表現すればいいじゃん?」
と思われるかもしれませんが、実はばらつき単体、例えば標準偏差などは平均値の大きさに引っ張られやすいという特性があるんです。なので標準偏差(つまりノイズ同士)を単純に比較することが出来ない。
このあたりは変動係数の概念を理解する必要がありますので、よく分らんという方はこちらの記事をどうぞ
「なるほど、ならばそれこそ変動係数で良いじゃないか。わざわざSN比という値をこさえる必要性が分からん」
この点ですが、これは加法性を与えるためという理由があります。
元々標準偏差そして平均値と標準偏差の比である変動係数には、加法性がありません。
加法性とはその名の通り足し算出来る性質の事。ひいては四則演算をするための性質です。(足し算できなきゃ引き算が出来ない。足し算が出来なきゃ掛け算も出来ない。掛け算も出来なきゃ割り算も出来ない)
実験というのは、測定をして、その測定値を分析して結果を考察するものです。分析をするためには平均値などといった統計量を割り出す必要がありますが、測定値が足し算できなければ基本的な平均値を出すことも出来ません。
故にばらつきに加法性を持たせないとばらつきの分析が出来ないのです。
ばらつきに加法性を持たせるには標準偏差を二乗する必要があります。分散値なら加法性があるのです。
しかし分散単独であれば、先述の平均値に引っ張られるというデメリットが発生するので、平均値との比を取った上で二乗する必要があります。
そしてここで更にもう一工夫なのですが、比の値というのはパーセントの世界。
パーセントは0%付近と50%付近で1%の価値が変わります。不良率を50%⇒49%は容易ですが、1%⇒0%はチョームズいですよね?
つまり単なる比では、加法性に不安が残る。
故に最後にこの平均値とばらつきの比を対数化することで、加法性を与えているのです。
この比を対数化することで加法性を与える方法はロジット変換(品質工学ではオメガ変換)と呼ばれており、ロジスティック回帰分析でも使われている概念です。
ロジスティック回帰分析を分かりやすく解説します【百分率を分析出来る重回帰分析】
つまり数式で表すと、
$$SN比=10\log_{10}\frac{Ave^2}{σ^2}$$
Aveが平均値でσがばらつきです。最初に10を掛けていますが、これは単に数字を大きくしてるだけで大した意味は持ってないです。
という事で、これがSN比の概略になります。
ただし実際には平均値や標準偏差を直接使用するわけではありません。動特性においては平均値の代わりに傾き、ばらつきは全変動から傾きの情報を抜いたものを使用し、計算式が相当に煩雑です。実際の式は
$$SN比=10\log_{10}{\frac{1/2r・(S_β-V_e)}{V_N}}$$
そしてSβ、Veなどの計算もまぁ色々やんなきゃなんない。一応SN比の数理に関する論文を記載しますが、
あまり真剣に読む気がしないというのが正直なところ。私のような製品開発が目的で、とりあえず良いものが出来あればええねんという方にとってはそのあたりの厳密さには興味が持てないと思います。
とりあえずは、変動係数の逆数に加法性を持たせた指数という事を理解できていれば十分でしょう。
従来型のSN比の問題点
さて、このSN比(エネルギー比型と比べるため、以下従来型と呼称します)には問題点があるというのが、エネルギー比型SN比(以下E型)が誕生することになった理由になります。
この従来型のデメリットは信号の数が変わると、SN比が変わってしまう点にあります。
信号3つと信号4つでは本質的なばらつきが同じでも、結果が変わる。
そして、信号が30,40,50と100,150,200でも結果が変わる。
信号が完全に一致しないと、再現性が取れないのです。
技術が単純だとこのあたりはそれほど大きな影響は無いです。
例えばLEDの機能性評価を行うのであれば、毎回流す電力を3水準でどの水準も一緒にしておけば問題ありません。
しかし、最近の製品開発でそのような信号因子の与え方で問題ない事例はそれほど多くないはずです。
現に私が今行っている製品開発はS-Sカーブで評価しているのですが、S-Sカーブで得られる信号(例えばストローク)は毎回数字が違います。そして信号数も毎回微妙に違います。
正に従来型の問題点にぶち当たる事案でして、大変困ったことを覚えています。
エネルギー比型SN比とは?
構造がシンプル
これらの問題点をE型は解消してくれる模様ですが、どうやるのでしょうか。
基本的な概念としては、全変動の中でシグナル以外は全部ノイズというシンプルなものを採用しています。
というのも、従来型はデータのばらつき、つまり全変動をシグナルによるもの、偶然誤差によるもの、誤差因子によるものの3つに分けています。
ですが、そもそも機能性評価によるSN比の評価のメリットは、誤差因子で無理矢理ばらつかせる事で、相対的に偶然誤差の影響を小さくしサンプルサイズを最小限にすることです。
つまりその概念に従うのであれば、偶然誤差の情報を計算する必要は無いのです。だって殆ど無視できるほど小さいのだから。
となれば、存在するのは全変動、シグナルによる変動、誤差因子による変動です。そしてこれらの関係を式で表すと
全変動=シグナル変動+誤差因子変動
になります。つまりこの3つの変動のうち2つが導ければ、必然的に全ての値が求まります。
E型では、全変動とシグナルによる変動のみを求め、誤差因子の変動は
誤差因子変動=全変動-シグナル変動
と表現します。非常にシンプルになりました。
実際の式としては
$$E型SN比=10\log_{10}(\frac{S_β}{S_T-S_β})$$
「そんなにシンプルになった?」と思われるかもしれませんが、実際に計算するとそのダイエットぶりに驚愕します。
自由度の計算が一切不要になるし、STの計算はただの出力値の二乗和なので実際にごちゃごちゃ計算するのはSβだけになります。VNとかVeの計算から完全に開放されるのはかなりデカいのです。
信号の数が違っても大丈夫
そしてE型の場合、信号因子の違いが合っても大丈夫みたいです。
そもそも従来型は式の構造上無次元数の対数ではなく、1/信号因子^2の対数になっているらしくこれが原因で、信号因子が2倍になると、SN比が4乗で小さくなるようです。

https://www.i-juse.co.jp/statistics/xdata/sympo25-tsuruta-document.pdfより抜粋
この文脈に従うならば、E型ではシグナルと誤差因子の比が無次元数になっており、信号因子の大きさに寄らないという事なのでしょう(このあたりの数理的な理解は私よく分ってない)。
実際に検証した際の事例も元の文献に記載されているので、気になる方はぜひ目を通してみてください。
非線形の時は信号を出来るだけ合わした方が良い
このあたりは私が実際に使用した時の体験談になります。
文献では信号の値が異なってもOKとありますが、おそらくこれは線形が理想である場合に限ります。
非線形の場合はおそらくダメです。
厳密に言うと、最後の水準の信号は出来るだけ近くないとダメです。
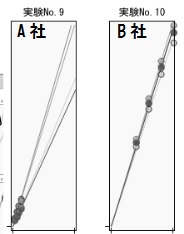
https://www.i-juse.co.jp/statistics/xdata/sympo25-tsuruta-document.pdfより抜粋
例えばこの事例の場合標準型では、信号因子の影響でA社の方がSN比が大きくなるといった結果が出るのに対して、E型の場合正しくB社の方がSN比が大きくなります。
一番大きい信号因子の水準が大きく異なるにもかかわらずです。
これがなぜ可能なのかと言えば、線形の機能であるので本来存在しない信号因子の出力が線を伸ばした先に存在するからです。
しかしながら非線形の場合、信号が一つ違うと別の方向に行ってしまいます。
信号因子が10の時出力が20だったとして、信号因子が11の時に22ではなく15となるのが非線形の機能です。延長線上に存在しないので、理想的な出力値が予測できないのです。
これは標準SN比のときのように、線形変換するときも同様です。標準となるグラフに存在しない信号の出力は予測できず、線形に変形出来ません。
なので、非線形機能を分析するときは末端を揃えてください。
厳密にそろえる必要はありません。ちょっとずれたぐらいなら対応出来ます。
ですが、文献の信号ズレの事例のような大きなズレは対応出来ないので注意してください。
まとめ
まだまだ事例としてはあまり見かけませんが、エネルギー比型SN比は非常に便利です。
式も分かりやすいので、計算ミスが起こりにくいですし、おおむね信号の端を合わせておけば線形だろうが非線形だろうが対応出来ます。
昨今信号を意図的に合わせられる事例は減っていっていると思います。
技術が進んでいるからです。
単純な開発はやり尽くされているからです。
そのような状況下故にSN比の適用が難しいから、品質工学を使わないというのは非常にもったいないです。
ぜひ、新しい手法を積極的に取り込んで、より良い製品をスピーディーに生み出していってください。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
また最近は私が実務で多用していることもあって品質工学の解説も始めました。
「いや、品質工学勉強したことがあるけど、機能?とかよく分らなくて結局使ってない」
そんな方向けにnoteで品質工学の論文を分かりやすく解説しています。
品質工学を使いこなすには、実用が一番なのですが、教科書⇒実用というのはどうにもハードルが高い。
そのハードルを低くするには、過去論文を読んで様々な機能の考え方に触れるのが一番なんです。
こんな感じで、様々なコンテンツを展開しています。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント