こんにちわ、熊野です。
皆さんは百分率のデータを扱う機会ってどれくらいありますか?
きっと沢山あるものと思います。
私が携わる製造業でも、不良率や歩留など百分率で表現する事が非常に多いです。
またマーケティングであれば、男女の比率や年齢の比率など様々な層別で分類する場合も百分率で表現していると思います。
なぜ、これほどまでに百分率が使用されるのか。それは総数が異なっていても比較することが出来るからです。
2021年と2020年でアンケートを取ったとして、獲得出来たサンプルサイズが同数になることはまずありえないと思います。100人 vs 150人とかざらにあるわけです。
このような場合百分率を使えば、同じ土俵で比率を比較出来るわけです。
異なるサンプルサイズであっても、10%とかの数字が持つ意味合いは変わらないのですから。
また、もう一つ使われる理由として0~100%の間の数字になるのでイメージしやすいという事が挙げられます。
不良数が500pcsとか1000pcsとか言われても、規模間はピンとこないと思いますが、百分率で表して5%とか10%と変換されれば非常に分かりやすいですよね。
このように取り得る数字がどの分野のデータでも同じになるので、こういった点でも百分率は解釈しやすいのです。
さてこの百分率、このようなメリットから多用されるわけですが、統計的に分析しようとすると実は結構クセがあります。
このクセの強さを理解せずに分析してしまうと、とんだ誤認識につながる可能性があるのです。
今回はこの百分率の問題点とそこをカバーするロジット変換、ロジスティック回帰分析を解説いたします。
動画でも解説しています。
百分率データの厄介さ

感覚で理解しよう
まずはこの百分率の厄介さを感覚的に理解してみましょう。
不良率を50%から45%にするのと、5%から0%にするのは同じ難易度と思われますか?
製造現場で改善に従事してきた方なら、即答で5%⇒0%が圧倒的に難しいと仰るはずです。
でも数字上は同じ5%の幅ですよね?
このように実は百分率は0から100%にかける全ての範囲で1%の価値が同じわけではないのです。
このあたりの感覚的なことをグラフでも確認してみましょう。
グラフで理解しよう
先ほどの1%の価値の違いをグラフで表すとこんな感じになります。
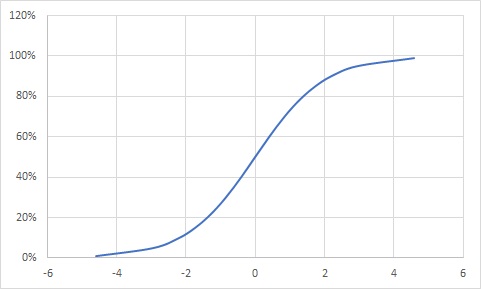
20~80%にかけての傾きと、0~20%および80~100%にかけての傾きが異なります。
先ほどの例と照らし合わせると、45%から50%は傾きが急ですが5%から0%は傾きがほとんどありません。
このように実は百分率は非線形の傾向を示すのです。そしてグラフが非線形であるという事は統計として扱うのが難しいという事でもあります。
統計学の基本的な手法は線形を前提としています。つまり
$$y=ax+b$$
このような関係性です。実験計画法や多変量解析も例外ではありません。
つまり非線形な百分率をそのまま統計の一般的な手法で分析するのは、基本不可能な訳なのです。
ロジット変換

百分率のデータを線形に変換する
百分率がそのままで扱えないのなら、何かしらの変形を施してやればよい訳です。
この百分率のデータを線形に変換する処理をロジット変換といいます。以下の式です。
$$Ln(\frac{P}{1-P})$$
Pには変換したい百分率のデータを入れます。この変換をすることで百分率を線形データとして扱うことが可能となります。
ただし注意点があります。それは0%と100%は変換が出来ないという事です。
0%の場合p/1-pが0になりますが、0を対数に変換することは出来ません。
また、100%の場合はそもそもp/1-pの分母が0になってしまい計算が成立しません。
このため0%や100%が計算に組み込まれる場合は、0や100に限りなく近い数値を代用する必要があります。
方法としてはこちらのサイトで非常に実践的な方法が提示されています。
例えば0,1,2,4,5%という集団があるとします。
このままでは0%が変換できません。であれば、0を除いた場合の最小値1を全ての集団に足してあげるのです。つまり
1,2,3,4,5,6%という集団にしてからロジット変換をしてあげるのです。
相対的な関係性はほとんど変わらないのですから、有効な変換方法という訳です。
このようにしてロジット変換をして線形の分析手法を適用すれば、百分率を分析することも可能になります。
ロジスティック回帰分析とは
最後にロジスティック回帰分析に触れておきます。
響きは難しそうでおっかないですが、何のことはありません。重回帰分析の目的変数yをロジット変換した百分率に置き換えただけのものです。
つまり
$$Ln(\frac{P}{1-P})=ax_1+bx_2+cx_3・・・$$
これがロジスティック回帰式です。重回帰分析なにそれ美味しいのって方は先にこちらをご覧ください。
この分析を使う事で、各説明変数が百分率のデータにどの程度の影響を及ぼしているのかを分析することが可能となります。
まとめ
百分率はどのような指標であっても0~100%というイメージしやすい指標で表現されるために、頻繁に活用されます。
しかしながら、そのままでは非線形な動きをするために統計的に分析することが難しいです。
この百分率はロジット変換を行うことで、線形の動きをするようになるので統計の一般的な手法で分析することが可能となります。
ロジスティック回帰分析だけでなく、相関分析も主成分分析も可能となります。
分析の手駒が一気に増えるわけです。
ぜひ使いこなせるようになって、データ分析の達人になりましょう。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。




コメント