何かデータを取り終わった際に、最初に算出する値は平均値でしょう。
統計手法を使う際でも、基本的に正規分布を前提とした手法が大半を占めるので、平均値と標準偏差の算出は、とりあえずやっておけというくらいに必須事項です。
そんな代表的な統計量である平均値ですが、皆さん
「サンプルサイズは一体いくらあればいいんだ?」
と疑問に思われた事ありませんか?
標準偏差でも30だの、いいや100だのとはっきりしないですが、平均値の場合特に言及されることが少なく、逆に不安に思っている方もいらっしゃるのではないでしょうか。
以前標準偏差のサンプルサイズを考えた時と同様に、今回は平均値のサンプルサイズについても考えてみましょう。
推定から逆算しよう
なぜ推定から考えるのか?
推定という手法は代表値(今回は平均値)がどのような信頼区間に収まるのかを導く手法です。
そして、その信頼区間を決定する要素は有意水準αとサンプルサイズnです。
有意水準は大抵0.05としますので、基本的にサンプルサイズによって平均値の信頼区間、つまり精度が決定します。
これは逆に言えば、求めている精度を得るために必要なサンプルサイズを求める事が出来るという事です。
平均値の区間推定
平均値の区間推定は、まずt値を算出します。
$$t=\frac{\overline{x}-μ}{s/\sqrt{n}}$$
このt値が、自由度によって決定したt分布の両側推定95%(1-有意水準0.05)に収まるのかを考えます。
$$Pr=[|t(n-1,0.05)| ≧ t]=0.95$$
$$Pr=[|t(n-1,0.05)| ≧ \frac{\overline{x}-μ}{s/\sqrt{n}}]=0.95$$
$$Pr=[\overline{x}-t(n-1,0.05)\frac{s}{\sqrt{n}} ≦ μ ≦\overline{x}+t(n-1,0.05)\frac{s}{\sqrt{n}}]=0.95$$
要は、サンプルサイズによって以下の補正値
$$t(n-1,0.05)\frac{s}{\sqrt{n}}$$
がどれだけ小さくなるのか、どの程度の小ささなら許容できるのかを見ていけば良いのです。
エクセルでグラフ化しよう
下準備です。
ここからはエクセルの力を借りましょう。
ただその前に前提条件として
$$s=1$$
とします。今回はサンプルサイズの影響を見るだけに終始したいためです。
となると、結局
$$\frac{t(n-1,0.05)}{\sqrt{n}}$$
を計算するという訳です。
エクセルでt値を算出するには?
エクセルでt(n-1,α)算出する関数は
=T.INV.2T(確率,自由度)
になります。なので、今回は
$$\frac{T.INV.2T(0.95,n-1)}{\sqrt{n}}$$
以上の数字をサンプルサイズnに対してプロットしたグラフを書くことになります。
結果としては、
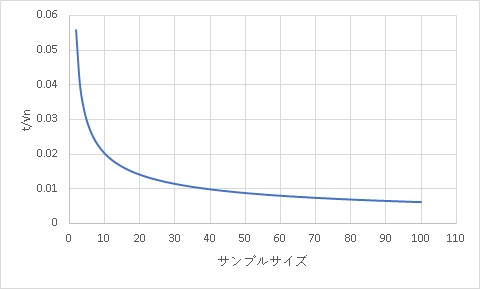
こうなりました。サンプルサイズ30時点から変化が収まっています。
実際にはこの値に標準偏差を乗するのですから、これで決定という訳ではありませんが、サンプルサイズの依存という面を見ると、N=30は揃えておくべきましれません。
サンプルサイズの注意点
平均値も推定から考えるとサンプルサイズ30はあった方が良いというような結果となりました。
もちろん標準偏差の値、そもそもどの程度の誤差なら許容出来るのかによりますが、個人的には思ったよりサンプルサイズが必要なんだなと意外に思っております。
ただ注意してほしいのですが、このサンプルサイズはt検定に必要なサンプルサイズとは異なるという点です。
正確な平均値を知る場合、サンプルサイズは多いに越したことはありません。
しかしながら検定の場合、サンプルサイズの増加で検出力が上がりすぎると、些細な差も有意差ありと第一種の過誤をしてしまう可能性が増大してしまいます。
つまり用途によって同じ統計量を対象としても、必要となるサンプルサイズは違うという事を常に意識してください。
ちなみに、正確な平均値を知り、かつ検定も正しく行いたい場合は、N=30を採取し多すぎる場合、エクセルの分析ツールサンプリングを用いて、ランダムにそこから必要な数抜き取って検定を行ってください。
うまくいくと思います。
まとめ
平均値もサンプルサイズとしては、30以上は必要みたいです。
ですが、実際にサンプルサイズ30を実施するというのは、結構しんどい場合も多いです。
何が何でもサンプルサイズを沢山取るんだと意気込む前に、
・必要な精度はどの程度?
・そもそも標準偏差はどの程度(これが小さかったら、サンプルサイズは小さく出来る)
をよく確認し、サンプリングを適切に設計しましょう。
大事なのは、今自分がどの程度の精度が必要で、故にこのくらいのサンプリングが必要であるかを把握することです。
当サイトを閲覧下さる皆さまは、日々より良い仕事が出来るようになりたいと思われているビジネスパーソンがメインだと思います。 でも「時間が無い」、「セミナー行くの面倒くさい」といった理由で中々学べていない方も多いと思います。 このビジネス動画学習サービスでは、いつでも、どこでもスマホ一つでビジネススキルを隙間時間で学ぶことが出来ます。 youtube紹介はこちら



コメント