検出力(1-β)は、検定の確からしさを設計する上で重要な指標です。
今回はその検出力を計算する方法を紹介します。
今回は概念を押さえるために、z検定の場合(つまり母分散既知)での検出力の計算方法を紹介します。
基本的な概念さえ押さえておけば、実際のt検定における検出力設定などはEZRなどの統計ソフトに任せても良いでしょう。
検出力をテーマとした書籍は非常に貴重です。勉強する際はちょっと難しいですがこちらを読んでみて下さい。
動画でも紹介しています
統計学がうまく使えなかった人はコチラ⇒統計学を活かす 解析しやすい数値化のノウハウ
検出力を計算しよう
検定条件の設定
まずはz検定の流れを見てみましょう。
H0:帰無仮説 $$μ_0=μ_1$$
H1:対立仮説 $$μ_0≠μ_1$$
有意水準α:0.05
正規分布を用いた母平均の検定の場合、検定統計量は
$$z_0=\frac{\overline{x}-μ_0}{\sqrt{σ^2_0/n}}$$
となります。このZ0が
$$|Z_0|>Z_{α/2}$$
となった場合H0を棄却して対立仮説を採択します。
これが母分散既知の平均値の検定である、z検定になります。
以前にも解説していますので、詳細を知りたい場合は以下の記事を参照してください。
検出力の計算
それでは本題に入ります。
検出力はH1:対立仮説が成り立つ前提で計算します。つまり
$$μ_0≠μ_1$$
という条件で計算するということです。
まず検出力1-βとは対立仮説が正しい場合に、対立仮説を採択する確率になります。

グラフで見ると、分かりやすいです。
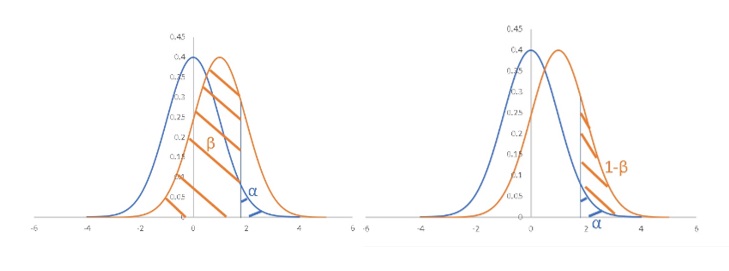
H0を前提にするというのは、青色分布に注目するという事。
そしてH1に注目するという事は橙色分布に注目するという事です。
青色と橙色分布の距離が離れるほど、1-βつまり対立仮説を採択する可能性が上昇するのです。
よって1-βの値は以下の式によって導かれます。
$$1-β=Pr(|Z_0|>Z_{α/2})$$
Prはカッコ()内が成立する確率を示します。つまりこの式は先ほどの帰無仮説を棄却する確率は1-βであるということを示しています。
次にこのPr()内を変形させていきます。
ここでZ0は先に示したように
$$z_0=\frac{\overline{x}-μ_0}{\sqrt{σ^2_0/n}}$$
ですので、
$$1-β=Pr(|Z_0|>Z_{α/2})=Pr(\frac{\overline{x}-μ_0}{\sqrt{σ^2_0/n}}≦-Z_{α/2})+Pr(\frac{\overline{x}-μ_0}{\sqrt{σ^2_0/n}}≧Z_{α/2})$$
となります。
これを変形すると
$$1-β=Pr(\frac{\overline{x}-μ_1}{\sqrt{σ^2_0/n}}+\frac{μ_1-μ_0}{\sqrt{σ^2_0/n}}≦-Z_{α/2})+Pr(\frac{\overline{x}-μ_1}{\sqrt{σ^2_0/n}}+\frac{μ_1-μ_0}{\sqrt{σ^2_0/n}}≧Z_{α/2})$$
になります。ここで重要なのが対立仮説
$$μ_0≠μ_1$$
を前提として変形させるという事です。
$$1-β=Pr(Z_1≦-Z_{α/2}-\sqrt{n}Δ)+Pr(Z_1≧Z_{α/2}-\sqrt{n}Δ)$$
ただし
$$Δ=\frac{μ_1-μ_0}{σ_0}$$
Δは効果量です。青色と橙色の分布の位置関係を示している値です。
$$Z_1=\frac{\overline{x}-μ_1}{\sqrt{σ^2_0/n}}$$
μ0と異なる(≠)μ1からなる検定統計量Z1が、ある値(不等式の右側)を下回る(or上回る)時に対立仮説が成り立つ確率、検出力の式が導出されました。
ちなみに帰無仮説が成り立つ際は以下の式、
$$1-β=Pr(\frac{\overline{x}-μ_1}{\sqrt{σ^2_0/n}}+\frac{μ_1-μ_0}{\sqrt{σ^2_0/n}}≦-Z_{α/2})+Pr(\frac{\overline{x}-μ_1}{\sqrt{σ^2_0/n}}+\frac{μ_1-μ_0}{\sqrt{σ^2_0/n}}≧Z_{α/2})$$
が、μ1-μ0何某の箇所において分子は0になるし![]() -μ1は
-μ1は![]() -μ0と同じ値になりますので、最初の式に戻ってしまいます。
-μ0と同じ値になりますので、最初の式に戻ってしまいます。
これは帰無仮説が成り立つ場合、1-β=αということを示しています。
検出力の式の使い方
基本的に検定の事前と事後に使用します。
検定前にはサンプルサイズを決定する
事前使用では、効果量Δを実績により任意に決定します。
また、検出力1-βは一般的には0.8で設定します。
有意水準αは0.05で設定します。
以上を決定すると、自動的にサンプルサイズnが決定されます。
このようにして、最適と思われるサンプルサイズを決定することが出来ます。
検定後に検定の確からしさをチェック
事前に設定した検出力とサンプルサイズは、設定した効果量が確かだった場合にのみ成り立ちます。
しかし実際には、効果量の実測値は設定値よりもズレますので、検定後にサンプルの効果量、サンプルサイズ、有意水準の値から検出力を算出します。
これで、検定がどれだけの検出力で実施されたのか確認できます。
また、この時の結果から検出力が足りていなかった場合は、効果量の実測値を利用して再度サンプルサイズを再算出して検定をやり直すことが出来ます。
まとめ
今回は検出力の計算方法から、使用法までを解説しました。
実際には、EZRで検出力やサンプルサイズは算出出来るので、実用をする場合には以下の記事を参照ください。
検定において、検出力の計算はエクセルにデフォルトで搭載されておらず、また書籍も少ないので耳慣れない方も多いと思います。
逆を言えば、他の人もめったに使えないという事です。
ここで当記事と書籍を活用して、ぜひマスターしてください。
コンテンツ紹介
昨今機械学習やディープラーニングなど、データを扱うための知識の重要度は日々増していっています。
そんな最先端のスキルを使いこなすには、土台となる統計学の知識が必要不可欠です。
しかしながら、統計学は本で読んでも何とか理論は理解できてもそこからどのように実務に活かしたら良いのか分からない。そんな机上と現実のギャップが凄まじい学問です。
そんな机上と現実のギャップを埋めるために、私は当サイトをはじめ様々なコンテンツを展開しています。
youtubeでは登録者1万人の統計学のチャンネルを運用しています。
動画投稿だけでなく、週2回のコメントに来た質問への回答配信も行っているので気になる方はどしどし質問をお寄せください。
youtubeでは無料動画だけでなく、有料のメンバーシップ限定動画も運用しています。
メンバーシップ登録リンク(押しただけで登録はされないので、気軽にクリックしてください)
エクセルやJAMOVIといった無料で使える統計ツールの実際の使い方。そして無料動画では敷居の高い(というよりマニアックゆえに再生数が見込めない(笑))解説動画をアップしています。
本を読んで実際に分析してみようと思ったけど、どうもうまくいかなかった。本では見かけない、あるいは難しすぎて扱えない手法があったという方。ぜひ一度ご参加ください(動画のリクエストがあれば反映させます)
「そうは言われても、うちのデータは統計学じゃ分析出来ないよ」
そういう方もいらっしゃると思います。私の経験上、そういったデータ分析が出来ない状況の一つとして量的変数として目の前の現象を扱えていないというものがあります。
私のnoteでは、過去私が製品開発を行う上で実践した分析しやすい数値の測定方法を公開しています。
私が開発活動する上で創意工夫を凝らして編み出してきたアイデアの数々を公開しています(私の知見が増えたら更新していきます)。本やネットではまず載っていません。うまい測定方法のアイデアが浮かばないという方はぜひこちらをご覧ください。
「いや、その前に使える手法を体系的に学びたいんだけど」
そんな方には、udemyの講座を推奨します。
初歩的な標準偏差から、実験計画法、多変量解析まで、実際に私が実用する上で本当に使用したことがある手法に絞って順序立てて解説しています。
どの手法が結局使えますのん?という方はぜひこちらをお求めください。
こんな感じで、様々なコンテンツを展開しています。
今後は品質工学や品質管理に重点を絞ったコンテンツなども発信していきます。
ぜひリクエストがありましたら、それらも反映させていきますのでまずはお気軽にご意見くださいな。





コメント